
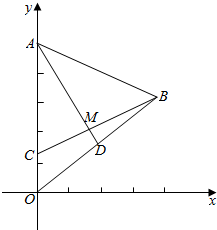
 如图所示,已知△AOB中,A(0,5),O(0,0),B(4,3),$\overrightarrow{OC}$=$\frac{1}{4}$$\overrightarrow{OA}$,$\overrightarrow{OD}$=$\frac{1}{2}$$\overrightarrow{OB}$,AD与BC相交于点M,求点M的坐标.
如图所示,已知△AOB中,A(0,5),O(0,0),B(4,3),$\overrightarrow{OC}$=$\frac{1}{4}$$\overrightarrow{OA}$,$\overrightarrow{OD}$=$\frac{1}{2}$$\overrightarrow{OB}$,AD与BC相交于点M,求点M的坐标. 分析 根据条件可以求出向量$\overrightarrow{OC},\overrightarrow{OD}$的坐标,从而得出点C,D的坐标,然后根据直线的两点式方程便可分别求出直线AD,BC的方程,联立这两个方程便可解出点M的坐标.
解答 解:$\overrightarrow{OC}=\frac{1}{4}\overrightarrow{OA}=\frac{1}{4}(0,5)=(0,\frac{5}{4})$,$\overrightarrow{OD}=\frac{1}{2}\overrightarrow{OB}=\frac{1}{2}(4,3)=(2,\frac{3}{2})$;
∴$C(0,\frac{5}{4}),D(2,\frac{3}{2})$;
∴直线AD的方程为$\frac{x-0}{2-0}=\frac{y-5}{\frac{3}{2}-5}$,即$y=-\frac{7}{4}x+5$;
直线BC的方程为$\frac{x-0}{4-0}=\frac{y-\frac{5}{4}}{3-\frac{5}{4}}$,即$y=\frac{7}{16}x+\frac{5}{4}$;
∴解方程组$\left\{\begin{array}{l}{y=-\frac{7}{4}x+5}\\{y=\frac{7}{16}x+\frac{5}{4}}\end{array}\right.$得,$\left\{\begin{array}{l}{x=\frac{12}{7}}\\{y=2}\end{array}\right.$;
∴点M的坐标为$(\frac{12}{7},2)$.
点评 考查向量坐标的数乘运算,以及起点在原点的向量坐标和终点坐标的关系,直线的两点式方程,两直线交点坐标和两直线方程形成方程组解的关系.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:选择题
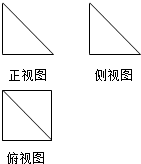 一个几何体的三视图如图所示,其中正视图和俯视图的都是腰长为1的两个全等的等腰直角三角形,则该几何体的体积为( )
一个几何体的三视图如图所示,其中正视图和俯视图的都是腰长为1的两个全等的等腰直角三角形,则该几何体的体积为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
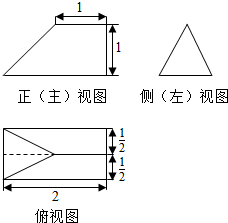
| A. | $\frac{5}{6}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com