
分析 把已知条件变形,然后作出可行域,在利用线性规划知识求解.
解答 解:由u>|v|,得$\left\{\begin{array}{l}{v≥0}\\{u>v}\end{array}\right.$或$\left\{\begin{array}{l}{v<0}\\{u>-v}\end{array}\right.$;
由2u=3(u2-v2),得$(u-\frac{1}{3})^{2}-{v}^{2}=\frac{1}{3}$.
作出可行域如图双曲线右支,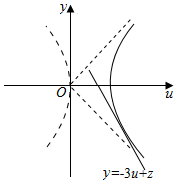
令z=3u+v,化为v=-3u+z,
联立$\left\{\begin{array}{l}{2u=3({u}^{2}-{v}^{2})}\\{v=-3u+z}\end{array}\right.$,消去v得:24u2+(2-18z)u+3z2=0.
由△=(2-18z)2-12×24z2=0,得9z2-18z+1=0.
解得:$z=\frac{3-2\sqrt{2}}{3}$(舍)或$z=\frac{3+2\sqrt{2}}{3}$.
∴3u+v的取值范围是[$\frac{3+2\sqrt{2}}{3},+∞$).
故答案为:[$\frac{3+2\sqrt{2}}{3},+∞$).
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法和数学转化思想方法,属中档题.


 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
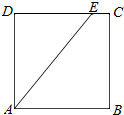 如图,在边长为2的正方形ABCD中,E为正方形边上的动点,现将△ADE所在平面沿AE折起,使点D在平面ABC上的射影H在直线AE上,当E从点D运动到C,再从C运动到B,则点H所形成轨迹的长度为π.
如图,在边长为2的正方形ABCD中,E为正方形边上的动点,现将△ADE所在平面沿AE折起,使点D在平面ABC上的射影H在直线AE上,当E从点D运动到C,再从C运动到B,则点H所形成轨迹的长度为π.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 组别 | 分组 | 频数 | 频率 |
| 第一组 | (50,60] | 10 | 0.1 |
| 第二组 | (60,70] | 20 | 0.2 |
| 第三组 | (70,80] | 40 | 0.4 |
| 第四组 | (80,90] | 25 | 0.25 |
| 第五组 | (90,100) | 5 | 0.05 |
| 合计 | 100 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com