
ЗжЮі ЃЈ1ЃЉЩшЭждВЕФБъзМЗНГЬЮЊЃК$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1ЃЈaЃОbЃО0ЃЉЃЎЩш|AF1|=mЃЌ|AF2|=nЃЌдђmnЁм3ЃЌгЩгкm+n=2aЃЌРћгУЛљБОВЛЕШЪНЕФаджЪЃКa2=3ЃЎгЩгквдЭждВCЕФгвНЙЕуЮЊдВаФЃЌНЙОрЮЊжБОЖЕФдВгыжБЯпl1ЃКx+$\sqrt{3}$y+1=0ЯрЧаЃЎПЩЕУ$\frac{|c+1|}{2}$=cЃЌcЃО0ЃЌНтЕУcЃЌПЩЕУb2=a2-c2ЃЎ
ЃЈ2ЃЉЕБжБЯпl2ЕФаБТЪДцдкЪБЃЌЩшжБЯпl2ЕФЗНГЬЮЊy=kx+mЃЌЯпЖЮPQЕФжаЕуMЃЈx0ЃЌy0ЃЉЃЎгыЭждВЗНГЬСЊСЂЛЏЮЊЃКЃЈ2+3k2ЃЉx2+6kmx+3m2-6=0ЃЌРћгУИљгыЯЕЪ§ЕФЙиЯЕМАЦфжаЕузјБъЙЋЪНПЩЕУЃК|ON|2=4|OM|2=$4ЃЈ{x}_{0}^{2}+{y}_{0}^{2}ЃЉ$ЃЌ|PQ|2=ЃЈ1+k2ЃЉ$[ЃЈ{x}_{1}+{x}_{2}ЃЉ^{2}-4{x}_{1}{x}_{2}]$ЃЎдЕуOЕНжБЯпPQЕФОрРыd=$\frac{|m|}{\sqrt{1+{k}^{2}}}$ЃЌЦНааЫФБпаЮOQNPЕФУцЛ§S=2ЁС$\frac{1}{2}$|PQ|•d=|PQ|•$\frac{|m|}{\sqrt{1+{k}^{2}}}$=$\sqrt{6}$ЃЌПЩЕУ|PQ|2=$\frac{6ЃЈ1+{k}^{2}ЃЉ}{{m}^{2}}$ЃЎЕУЕНmгыkЕФЙиЯЕЃЌДњШы|ON|2+|PQ|2ЃЌМДПЩжЄУїЃЎЕБжБЯпl2ЕФаБТЪВЛДцдкЪБЃЌЭЌбљГЩСЂЃЎ
НтД№ ЃЈ1ЃЉНтЃКЩшЭждВЕФБъзМЗНГЬЮЊЃК$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1ЃЈaЃОbЃО0ЃЉЃЎ
Щш|AF1|=mЃЌ|AF2|=nЃЌдђmnЁм3ЃЌ
Ёпm+n=2aЁн2$\sqrt{mn}$ЃЌЕБЧвНіЕБm=nЪБШЁЕШКХЃЌa2=3ЃЎ
ЁпвдЭждВCЕФгвНЙЕуЮЊдВаФЃЌНЙОрЮЊжБОЖЕФдВгыжБЯпl1ЃКx+$\sqrt{3}$y+1=0ЯрЧаЃЎ
Ёр$\frac{|c+1|}{2}$=cЃЌcЃО0ЃЌНтЕУc=1ЃЌ
Ёрb2=a2-c2=2ЃЎ
ЁрЭждВCЕФБъзМЗНГЬЮЊ$\frac{{x}^{2}}{3}+\frac{{y}^{2}}{2}$=1ЃЎ
ЃЈ2ЃЉжЄУїЃКЕБжБЯпl2ЕФаБТЪДцдкЪБЃЌЩшжБЯпl2ЕФЗНГЬЮЊy=kx+mЃЌЯпЖЮPQЕФжаЕуMЃЈx0ЃЌy0ЃЉЃЎ
СЊСЂ$\left\{\begin{array}{l}{y=kx+m}\\{\frac{{x}^{2}}{3}+\frac{{y}^{2}}{2}=1}\end{array}\right.$ЃЌЛЏЮЊЃКЃЈ2+3k2ЃЉx2+6kmx+3m2-6=0ЃЌ
ЁїЃО0ЃЌПЩЕУx1+x2=-$\frac{6km}{2+3{k}^{2}}$ЃЌx1x2=$\frac{3{m}^{2}-6}{2+3{k}^{2}}$ЃЎ
Ёрx0=$\frac{{x}_{1}+{x}_{2}}{2}$=$\frac{-3km}{2+3{k}^{2}}$ЃЌy0=kx0+m=$\frac{2m}{2+3{k}^{2}}$ЃЎ
Ёр|ON|2=4|OM|2=$4ЃЈ{x}_{0}^{2}+{y}_{0}^{2}ЃЉ$=$\frac{4{m}^{2}ЃЈ9{k}^{2}+4ЃЉ}{ЃЈ2+3{k}^{2}ЃЉ^{2}}$ЃЎ
|PQ|2=ЃЈ1+k2ЃЉ$[ЃЈ{x}_{1}+{x}_{2}ЃЉ^{2}-4{x}_{1}{x}_{2}]$=ЃЈ1+k2ЃЉ$[\frac{36{k}^{2}{m}^{2}}{ЃЈ2+3{k}^{2}ЃЉ^{2}}-\frac{4ЃЈ3{m}^{2}-6ЃЉ}{2+3{k}^{2}}]$=$\frac{12ЃЈ4+6{k}^{2}-2{m}^{2}ЃЉ}{ЃЈ2+3{k}^{2}ЃЉ^{2}}$ЁСЃЈ1+k2ЃЉЃЎ
Ёр|ON|2+|PQ|2=$\frac{12{m}^{2}{k}^{2}+120{k}^{2}+72{k}^{4}-8{m}^{2}+48}{ЃЈ2+3{k}^{2}ЃЉ^{2}}$ЃЎ
дЕуOЕНжБЯпPQЕФОрРыd=$\frac{|m|}{\sqrt{1+{k}^{2}}}$ЃЌ
ЦНааЫФБпаЮOQNPЕФУцЛ§S=2ЁС$\frac{1}{2}$|PQ|•d=|PQ|•$\frac{|m|}{\sqrt{1+{k}^{2}}}$=$\sqrt{6}$ЃЌ
Ёр|PQ|2=$\frac{6ЃЈ1+{k}^{2}ЃЉ}{{m}^{2}}$ЃЎ
Ёр$\frac{12ЃЈ4+6{k}^{2}-2{m}^{2}ЃЉ}{ЃЈ2+3{k}^{2}ЃЉ^{2}}$ЁСЃЈ1+k2ЃЉ=$\frac{6ЃЈ1+{k}^{2}ЃЉ}{{m}^{2}}$ЃЌЛЏЮЊЃК2m2=2+3k2ЃЎ
ДњШы|ON|2+|PQ|2=$\frac{ЃЈ2+3{k}^{2}ЃЉЃЈ6{k}^{2}-4ЃЉ+120{k}^{2}+72{k}^{4}+48}{ЃЈ2+3{k}^{2}ЃЉ^{2}}$=10ЃЎ
Ёр|ON|2+|PQ|2ЮЊЖЈжЕ10ЃЎ
ЕБжБЯпl2ЕФаБТЪВЛДцдкЪБЃЌЭЌбљГЩСЂЃЎ
злЩЯПЩЕУЃК|ON|2+|PQ|2ЮЊЖЈжЕ10ЃЎ
ЕуЦР БОЬтПМВщСЫЭждВЕФЖЈвхБъзМЗНГЬМАЦфаджЪЁЂжБЯпгыЭждВЯрНЛЮЪЬтЁЂжБЯпгыдВЯрЧаЮЪЬтЁЂвЛдЊЖўДЮЗНГЬЕФИљгыЯЕЪ§ЕФЙиЯЕЁЂЦНааЫФБпаЮЕФУцЛ§МЦЫуЙЋЪНЁЂЕуЕНжБЯпЕФОрРыЙЋЪНЙЋЪНЁЂЯвГЄЙЋЪНЁЂЛљБОВЛЕШЪНЕФаджЪЃЌПМВщСЫЭЦРэФмСІгыМЦЫуФмСІЃЌЪєгкФбЬтЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | ЮоНт | BЃЎ | гавЛНт | CЃЎ | гаСННт | DЃЎ | НтЕФИіЪ§ВЛШЗЖЈ |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
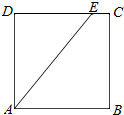 ШчЭМЃЌдкБпГЄЮЊ2ЕФе§ЗНаЮABCDжаЃЌEЮЊе§ЗНаЮБпЩЯЕФЖЏЕуЃЌЯжНЋЁїADEЫљдкЦНУцбиAEелЦ№ЃЌЪЙЕуDдкЦНУцABCЩЯЕФЩфгАHдкжБЯпAEЩЯЃЌЕБEДгЕуDдЫЖЏЕНCЃЌдйДгCдЫЖЏЕНBЃЌдђЕуHЫљаЮГЩЙьМЃЕФГЄЖШЮЊІаЃЎ
ШчЭМЃЌдкБпГЄЮЊ2ЕФе§ЗНаЮABCDжаЃЌEЮЊе§ЗНаЮБпЩЯЕФЖЏЕуЃЌЯжНЋЁїADEЫљдкЦНУцбиAEелЦ№ЃЌЪЙЕуDдкЦНУцABCЩЯЕФЩфгАHдкжБЯпAEЩЯЃЌЕБEДгЕуDдЫЖЏЕНCЃЌдйДгCдЫЖЏЕНBЃЌдђЕуHЫљаЮГЩЙьМЃЕФГЄЖШЮЊІаЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
| зщБ№ | Зжзщ | ЦЕЪ§ | ЦЕТЪ |
| ЕквЛзщ | ЃЈ50ЃЌ60] | 10 | 0.1 |
| ЕкЖўзщ | ЃЈ60ЃЌ70] | 20 | 0.2 |
| ЕкШ§зщ | ЃЈ70ЃЌ80] | 40 | 0.4 |
| ЕкЫФзщ | ЃЈ80ЃЌ90] | 25 | 0.25 |
| ЕкЮхзщ | ЃЈ90ЃЌ100ЃЉ | 5 | 0.05 |
| КЯМЦ | 100 | 1 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
 дкГЄЗНЬхABCD-A1B1C1D1жаЃЌAB=AD=1ЃЌAA1=2ЃЌИјГівдЯТУќЬтЃК
дкГЄЗНЬхABCD-A1B1C1D1жаЃЌAB=AD=1ЃЌAA1=2ЃЌИјГівдЯТУќЬтЃКВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com