
已知数列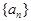 是等差数列,且
是等差数列,且 ,
, ,
,
(1)求数列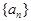 的通项公式; (2)令
的通项公式; (2)令 ,求数列
,求数列 前n项和
前n项和 .
.
(1)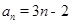 (2)
(2)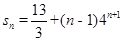
解析试题分析:解:(1)数列{an}是等差数列,且a1=1,a1+a2+a3=12,设出公差为d,∴a1+a1+d+a1+2d=12,∴a1+d=4,可得2+d=4,解得d=2,∴an=a1+(n-1)d=1+(n-1)×2=2n+1,(2)数列{an}的通项公式为an=n•2n,设其前n项和为Sn,∴Sn=1•21+2•22+3•23+…+n•2n①
2Sn=1•22+2•23+3•24+…+n•2n+1②
①-②可得-Sn=21+22+23+…+2n-n•2n+1②
∴-Sn=-2+22+23++…+2n -n•2n+1,
∴Sn=n×2n+1-2n+1+2=(n-1)2n+1+2;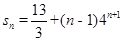
考点:等差数列,数列的求和
点评:主要是考查了等差数列的定义,以及通项公式的运用,以及错位相减法来求解数列的和,属于中档题。


 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com