练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    下列函数中，既是偶函数，又在上是单调减函数的是

    （A）                       （B）

    （C）                   （D）


    D


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    如图，已知正三角形的边长为6，将△沿边上的高线折起，使，得到三棱锥.动点在边上.

    （1）求证: 平面；

    （2）当点为的中点时，求异面直线所成角的正切值；

    （3）求当直线与平面所成角最大时的正切值.

     


    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设函数.

    （Ⅰ）当时，求函数的图象在点处的切线方程；

    （Ⅱ）已知，若函数的图象总在直线的下方，求的取值范围；

    （Ⅲ）记为函数的导函数．若，试问：在区间上是否存在（）个正数…，使得成立？请证明你的结论.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数，则              .

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知动点到点的距离等于点到直线的距离，点的轨迹为.

       (Ⅰ)求轨迹的方程；

       (Ⅱ)设为直线上的点，过点作曲线的两条切线,，

    （ⅰ）当点时，求直线的方程；

    （ⅱ）当点在直线上移动时，求的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     若函数，则______．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    2014年5月，北京市提出地铁分段计价的相关意见，针对“你能接受的最高票价是多少？”这个问题，在某地铁站口随机对50人进行调查，调查数据的频率分布直方图及被调查者中35岁以下的人数与统计结果如下：

    （Ⅰ）根据频率分布直方图,求a的值，并估计众数，说明此众数的实际意义；

    （Ⅱ）从“能接受的最高票价”落在 [8，10)，[10，12]的被调查者中各随机选取3人进行追踪调查，记选中的6人中35岁以上（含35岁）的人数为X，求随机变量X的分布列及数学期望． 

    最高票价

    35岁以下人数

    [2，4)

    2

    [4，6)

    8

    [6，8)

    12

    [8，10)

    5

    [10，12]

    3

         频率

         组距

    0.2
     

    a
     


    0.06
     

    0.06
     
                                                        

    0.04
     

    2
     
                                         

    10
     

    8
     

    6
     

    4
     
                            最高票价(元)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数的图象是


    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若函数f（x）在定义域D内某区间I上是增函数，且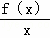在I上是减函数，则称y=f（x）在I 上是“弱增函数”．已知函数h（x）=x2﹣（b﹣1）x+b在（0，1]上是“弱增函数”，则实数b的值为(　　)

    查看答案和解析>>

    同步练习册答案