
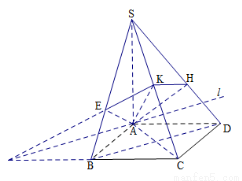
如图,四棱锥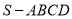 的底面是正方形,侧棱
的底面是正方形,侧棱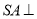 底面
底面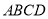 ,过
,过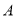 作
作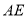 垂直
垂直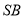 交
交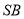 于
于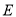 点,作
点,作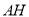 垂直
垂直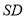 交
交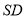 于
于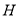 点,平面
点,平面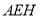 交
交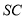 于
于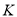 点,且
点,且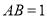 ,
,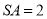 .
.
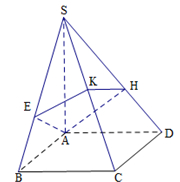
(1)设点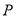 是
是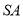 上任一点,试求
上任一点,试求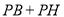 的最小值;
的最小值;
(2)求证: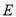 、
、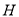 在以
在以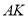 为直径的圆上;
为直径的圆上;
(3)求平面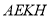 与平面
与平面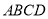 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
(1)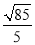 ;(2)详见解析;(3)
;(2)详见解析;(3)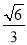 .
.
【解析】
试题分析:(1)将侧面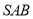 和侧面
和侧面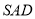 沿着
沿着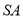 展开至同一平面上,利用
展开至同一平面上,利用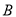 、
、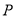 、
、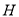 三点共线结合余弦定理求出
三点共线结合余弦定理求出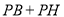 的最小值,即线段
的最小值,即线段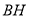 的长度;(2)证
的长度;(2)证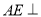 平面
平面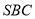 ,从而得到
,从而得到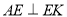 ,同理得到
,同理得到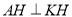 ,进而证明
,进而证明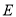 、
、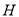 在以
在以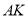 为直径的圆上;(3)方法一是建立以点
为直径的圆上;(3)方法一是建立以点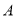 为坐标原点,分别以
为坐标原点,分别以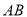 、
、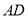 、
、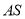 所在的直线为
所在的直线为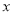 、
、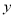 、
、 轴的空间直角坐标系,利用空间向量法求平面
轴的空间直角坐标系,利用空间向量法求平面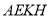 与平面
与平面 所成的锐二面角的余弦值;方法二是延长
所成的锐二面角的余弦值;方法二是延长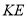 与
与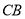 使得它们相交,找出二面角的棱,然后利用三垂线法找出平面
使得它们相交,找出二面角的棱,然后利用三垂线法找出平面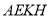 与平面
与平面 所成的锐二面角的平面角,利用直角三角函数来求相应角的余弦值.
所成的锐二面角的平面角,利用直角三角函数来求相应角的余弦值.
试题解析:(1)将侧面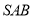 绕侧棱
绕侧棱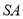 旋转到与侧面
旋转到与侧面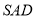 在同一平面内,如下图示,
在同一平面内,如下图示,
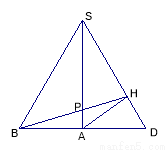
则当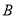 、
、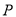 、
、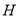 三点共线时,
三点共线时,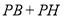 取最小值,这时,
取最小值,这时,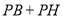 的最小值即线段
的最小值即线段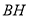 的长,
的长,
设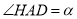 ,则
,则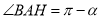 ,
,
在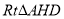 中,
中,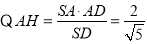 ,
,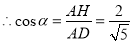 ,
,
在三角形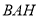 中,有余弦定理得:
中,有余弦定理得:
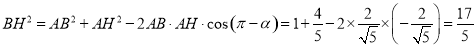 ,
,
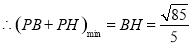 ,
,
(2)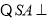 底面
底面 ,
,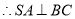 ,又
,又
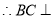 平面
平面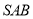 ,又
,又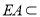 平面
平面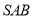 ,
,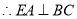 ,
,
又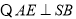 ,
,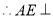 平面
平面 ,
,
又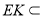 平面
平面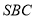 ,
,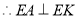 ,
,
同理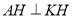 ,
,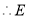 、
、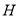 在以
在以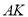 为直径的圆上;
为直径的圆上;
(3)方法一:如图,以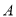 为原点,分别以
为原点,分别以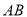 、
、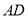 、
、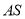 所在的直线为
所在的直线为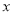 、
、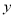 、
、 轴,建立空间直角坐标系如下图示,则
轴,建立空间直角坐标系如下图示,则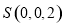 ,
,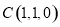 ,由(1)可得
,由(1)可得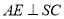 ,
,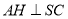 ,
,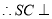 平面
平面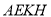 ,
,
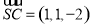 为平面
为平面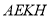 的一个法向量,
的一个法向量,
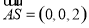 为平面
为平面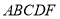 的一个法向量,
的一个法向量,
设平面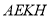 与平面
与平面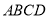 所成的锐二面角的平面角为
所成的锐二面角的平面角为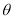 ,
,
则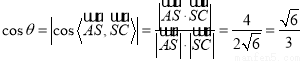 ,
,
 平面
平面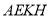 与平面
与平面 所成的锐二面角的余弦值
所成的锐二面角的余弦值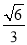 ;
;
方法二: 由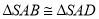 可知
可知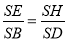 ,故
,故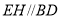 ,
,
又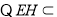 面
面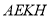 ,
,
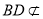 面
面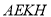 ,
,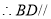 面
面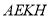 ,
,
设平面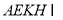 平面
平面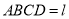 ,
,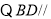 平面
平面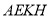 ,
,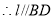 ,
,
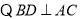 ,
,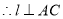 ,
,
又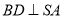 ,
,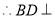 平面
平面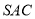 ,又
,又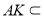 平面
平面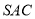 ,
,
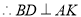 ,
,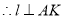 ,
,
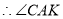 为平面
为平面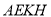 与平面
与平面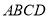 所成的锐二面角的一个平面角,
所成的锐二面角的一个平面角,
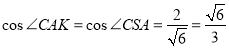 ,
,
 平面
平面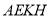 与平面
与平面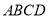 所成的锐二面角的余弦值为
所成的锐二面角的余弦值为 .
.
考点:1.空间几何体侧面展开图的应用;2.余弦定理;3.直线与平面垂直;4.空间向量法求二面角;5.三垂线法求二面角


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2013-2014学年广东省揭阳市高三4月第二次模拟考试理科数学试卷(解析版) 题型:选择题
已知命题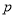 :函数
:函数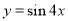 是最小正周期为
是最小正周期为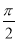 的周期函数,命题
的周期函数,命题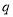 :函数
:函数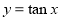 在
在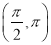 上单调递减,则下列命题为真命题的是( )
上单调递减,则下列命题为真命题的是( )
A.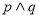 B.
B.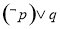 C.
C.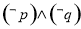 D.
D.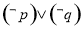
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省揭阳市高三4月第二次模拟考试文科数学试卷(解析版) 题型:选择题
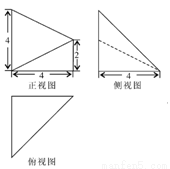
已知一棱锥的三视图如图所示,其中侧视图和俯视图都是等腰直角三角形,正视图为直角梯
形,正视图为直角梯形,则该棱锥的体积为( )
A.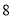 B.
B.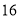 C.
C.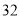 D.
D.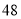
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省揭阳市高三4月第二次模拟考试文科数学试卷(解析版) 题型:选择题
某校有男、女生各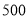 名,为了解男女学生在学习兴趣与业余爱好方面是否存在显著差异,拟从全体学生中抽取
名,为了解男女学生在学习兴趣与业余爱好方面是否存在显著差异,拟从全体学生中抽取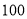 名学生进行调查,则宜采用的抽样方法是 ( )
名学生进行调查,则宜采用的抽样方法是 ( )
A.抽签法 B.随机数法 C.系统抽样法 D.分层抽样法
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省揭阳市高三3月第一次模拟考试理科数学试卷(解析版) 题型:选择题
如图所示的程序框图,能使输入的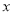 值与输出的
值与输出的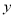 值相等的
值相等的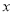 值个数为( )
值个数为( )

A.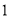 B.
B.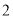 C.
C.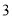 D.
D.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省揭阳市高三3月第一次模拟考试文科数学试卷(解析版) 题型:选择题
从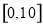 中任取一个数
中任取一个数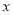 ,从
,从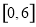 中任取一个数
中任取一个数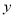 ,则使
,则使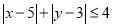 的概率为( )
的概率为( )
A.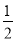 B.
B.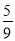 C.
C.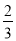 D.
D.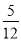
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省广州市毕业班综合测试二理科数学试卷(解析版) 题型:填空题
已知四边形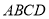 是边长为
是边长为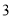 的正方形,若
的正方形,若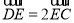 ,
,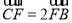 ,则
,则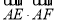 的值为.
的值为.
已知四边形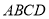 是边长为
是边长为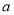 的正方形,若
的正方形,若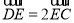 ,
,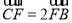 ,则
,则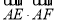 的值为.
的值为.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com