练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如图，四面体P-ABC，PA、PB、PC两两垂直，PA=PB=2，PC=4，E是AB的中点，F是CE的中点.

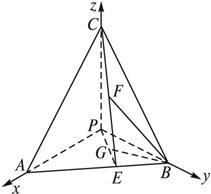
    (1)写出点B、C、E、F的坐标；

    (2)求BF与底面ABP所成的角的余弦值.

    解：(1)如图, 以PA为x轴, PB为y轴, PC为z轴, P为原点建立直角坐标系, 则B点坐标为(0, 2, 0), C点坐标为(0, 0, 4), A点坐标为(2, 0, 0).

    ∵E为AB中点,

    ∴E(1, 1, 0).

    ∵F为CE中点,

    ∴F(,, 2).

    (2)设G为PE中点, 则G(,, 0).

    ∵PA、PB、PC两两互相垂直,

    ∴PC⊥面ABP.

    ∵F、G分别为CE、PE中点,

    ∴FG∥PC.

    ∴FG⊥面ABP.

    故∠FBG为BF与面ABP所成的角.

    ∴, , .

    ∴.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：“伴你学”新课程　数学·选修1－2(人教B版) 人教B版 题型：022

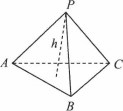
    在Rt△ABC中，CA⊥CB，斜边AB上的高为h1，则；类比此性质，如图在四面体P－ABC中，若PA、PB、PC两两垂直，底面ABC上的高为h，则得到的正确结论为________．

    查看答案和解析>>

    科目：高中数学 来源：设计选修数学2-1苏教版 苏教版 题型：013

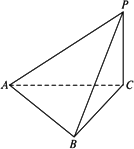
    如图，四面体P－ABC中，PC⊥面ABC，AB＝BC＝CA＝PC，那么二面角BAPC的余弦值为

    [　　]
    A．

    B．

    C．

    D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图,在四面体P—ABC中,已知PA=BC=6,PC=AB=10,AC=8,PB=2,F是线段PB上一点,CF=,点E在线段AB上,且EF⊥PB.

    (1)证明PB⊥平面CEF;

    (2)求二面角B—CE—F的大小.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

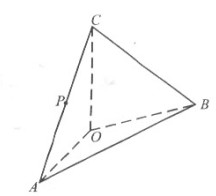
    如图, 在四面体ABOC中，OC⊥OA, OC⊥OB,∠AOB=120°，且OA=OB=OC=1.(Ⅰ) 设P为AC的中点.证明：在AB上存在一点Q,使PQ⊥OA,并计算=的值；(Ⅱ) 求二面角O-AC-B的平面角的余弦值. 

    查看答案和解析>>

    同步练习册答案