

(1)证明PB⊥平面CEF;
(2)求二面角B—CE—F的大小.
(1)证明:∵PA2+AC2=36+64=100=PC2,
∴△PAC是以∠PAC为直角的直角三角形.
同理,可证△PAB是以∠PAB为直角的直角三角形,△PCB是以∠PCB为直角的直角三角形.
故PA⊥平面ABC.
又∵S△PBC=![]() |PC||BC|=
|PC||BC|=![]() ×10×6=30,
×10×6=30,
而![]() |PB||CF|=
|PB||CF|=![]() ×2
×2![]() ×
×![]() =30=S△PBC.故CF⊥PB.又已知EF⊥PB,
=30=S△PBC.故CF⊥PB.又已知EF⊥PB,
∴PB⊥平面CEF.
(2)解:由(1)知PB⊥CE,PA⊥平面ABC,
∴AB是PB在平面ABC上的射影.
故AB⊥CE.
在平面PAB内,过点F作FF1垂直AB且交AB于F1点,则FF1⊥平面ABC,
EF1是EF在平面ABC上的射影.∴EF⊥EC.
故∠FEB是二面角B—CE—F的平面角;tan∠FEB=cot∠PBA=![]() ;
;
故二面角B—CE—F的大小为arctan![]() .
.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:
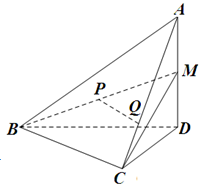 (2013•浙江)如图,在四面体A-BCD中,AD⊥平面BCD,BC⊥CD,AD=2,BD=2
(2013•浙江)如图,在四面体A-BCD中,AD⊥平面BCD,BC⊥CD,AD=2,BD=2| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 给出以下判断:
给出以下判断:| x2 |
| 4 |
| y2 |
| 3 |
 |
| y |
 |
| b |
 |
| a |
. |
| x |
. |
| y |
| AE |
| AB |
| 1 |
| 2 |
| AC |
| 2 |
| 3 |
| AD |
| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
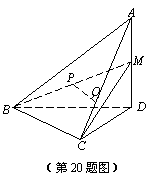
如图,在四面体A−BCD中,AD^平面BCD,BC^CD,AD=2,BD=2![]() .M是AD的中点,P是BM的中点,点Q在线段AC上,且AQ=3QC.
.M是AD的中点,P是BM的中点,点Q在线段AC上,且AQ=3QC.
(Ⅰ)证明:PQ∥平面BCD;
(Ⅱ)若二面角C−BM−D的大小为60°,求ÐBDC的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com