
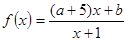 在(0,+
在(0,+ )上是增函数;命题q:方程
)上是增函数;命题q:方程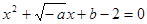 有两个不相等的负实数根,若p
有两个不相等的负实数根,若p q是真命题。
q是真命题。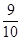 (2) (7,
(2) (7, 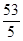 )
) f(x) =
f(x) =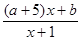 ,f ′(x)=
,f ′(x)= 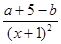 ,
,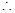 p真
p真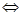 x
x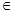 (0,+
(0,+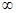 )时,
)时,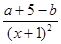 >0
>0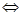 a-b+5>0,(2′)
a-b+5>0,(2′)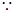 方程x2+
方程x2+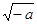 x+b-2=0有两个不相等的负实数根
x+b-2=0有两个不相等的负实数根
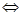
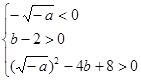
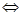
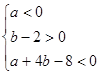 ,
,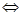
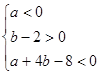 ; 5分
; 5分 q是真命题。则p真q真,
q是真命题。则p真q真,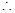
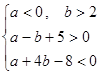 点P(a,b)的轨迹图形如图,
点P(a,b)的轨迹图形如图, ABC
ABC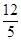 ,
,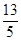 )
)
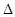 ABC的面积S=
ABC的面积S=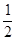
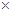 3
3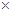 (
(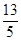 -2)=
-2)=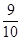 ,
, 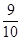 ; 10分
; 10分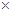 2=7,直线a+5b=z过C点时,
2=7,直线a+5b=z过C点时,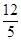 +5
+5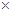
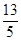 =
=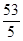 ,
,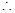 a+5b的取值范围是(7,
a+5b的取值范围是(7, 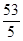 ) 13分
) 13分

 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com