
 PM2.5��ָ������ֱ��С�ڻ����2.5�Ŀ����Ҳ�ƿ���ο������Ϊ��̽����������PM2.5��Ũ���Ƿ���أ��ֲɼ���ij������һ������ijһʱ��γ�������PM2.5�����������
PM2.5��ָ������ֱ��С�ڻ����2.5�Ŀ����Ҳ�ƿ���ο������Ϊ��̽����������PM2.5��Ũ���Ƿ���أ��ֲɼ���ij������һ������ijһʱ��γ�������PM2.5�����������| ʱ�� | ��һ | �ܶ� | ���� | ���� | ���� |
| ������x�������� | 50 | 51 | 54 | 57 | 58 |
| PM2.5��Ũ��y����/�����ף� | 69 | 70 | 74 | 78 | 79 |
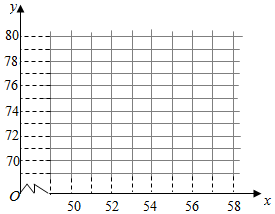
���� ��1��������㷨�ɵ����ݵ�ɢ��ͼ��
��2�����ݹ�ʽ���b��a����д�����Իع鷽�̣�
��3�����ݣ�2�����Իع鷽�̣�����x=25���PM2.5��Ũ�ȣ�
���  �⣺��1��ɢ��ͼ��ͼ��ʾ������2�֣�
�⣺��1��ɢ��ͼ��ͼ��ʾ������2�֣�
��2��$\overline{x}=\frac{50+51+54+57+58}{5}=54$��$\overline{y}=\frac{69+70+74+78+79}{5}=74$������6�֣�
$\sum_{i=1}^{5}��{x}_{i}-\overline{x}����{y}_{i}-\overline{y}��=4��5+3��4+3��4+4��5$=64��$\sum_{i=1}^{5}��{x}_{i}-\overline{x}��^{2}=��-4��^{2}+��-3��^{2}+{3}^{2}+{4}^{2}$=50��
$\widehat{b}=\frac{\sum_{i=1}^{5}��{x}_{i}-\overline{x}����{y}_{i}-\overline{y}��}{\sum_{i=1}^{5}��{x}_{i}-\overline{x}��}=\frac{64}{50}=1.28$��
$\widehat{a}=\overline{y}-b\overline{x}=74-1.28��54=4.88$������9�֣�
��y����x�����Իع鷽���ǣ�$\widehat{y}=1.28x+4.8$8����10�֣�
��3����x=2.5ʱ��y=1.28��25+4.88=36.88��37
���Կ���Ԥ���ʱPM2.5��Ũ��ԼΪ37����12�֣�
���� ������Ҫ���������Իع�����ķ���������ɢ��ͼ������С���˷���������Լ��ûع鷽�̽���Ԥ���֪ʶ�������˿������ݴ���������������


 �����ҵ���������ϵ�д�
�����ҵ���������ϵ�д� �����̸�Ӯ����ٸ�Ч�����ܸ�ϰ���ϿƼ�������ϵ�д�
�����̸�Ӯ����ٸ�Ч�����ܸ�ϰ���ϿƼ�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{2}$f��$\frac{��}{3}$����$\sqrt{2}$f��$\frac{��}{4}$����$\sqrt{3}$f��$\frac{��}{4}$����$\sqrt{3}$f��$\frac{��}{3}$�� | B�� | $\sqrt{2}$f��$\frac{��}{4}$����$\sqrt{2}$f��$\frac{��}{3}$����$\sqrt{3}$f��$\frac{��}{3}$����$\sqrt{3}$f��$\frac{��}{4}$�� | ||
| C�� | $\sqrt{2}$f��$\frac{��}{4}$����$\sqrt{2}$f��$\frac{��}{3}$����$\sqrt{3}$f��$\frac{��}{4}$����$\sqrt{3}$f��$\frac{��}{3}$�� | D�� | $\sqrt{2}$f��$\frac{��}{4}$����$\sqrt{3}$f��$\frac{��}{4}$����$\sqrt{2}$f��$\frac{��}{3}$����$\sqrt{3}$f��$\frac{��}{3}$�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 80 | B�� | 100 | C�� | 120 | D�� | 160 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
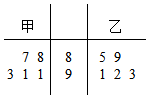 Ϊ�˲μӻ�ѧ������ijУ�ڼס���������ѧ�س�С���зֱ�ѡ��5��ѧ���μӱ���������ȡ�õijɼ�������100�֣��ľ�Ҷͼ��ͼ��ʾ��
Ϊ�˲μӻ�ѧ������ijУ�ڼס���������ѧ�س�С���зֱ�ѡ��5��ѧ���μӱ���������ȡ�õijɼ�������100�֣��ľ�Ҷͼ��ͼ��ʾ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
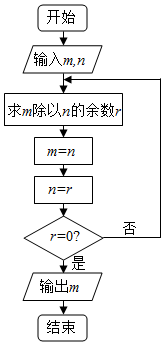
| A�� | 2 | B�� | 17 | ||
| C�� | 34 | D�� | ���ϴ𰸶�����ȷ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com