
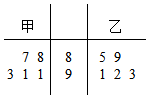
 为了参加化学竞赛,某校在甲、乙两个化学特长小组中分别选出5名学生参加比赛,他们取得的成绩(满分100分)的茎叶图如图所示:
为了参加化学竞赛,某校在甲、乙两个化学特长小组中分别选出5名学生参加比赛,他们取得的成绩(满分100分)的茎叶图如图所示:分析 (1)根据茎叶图中的数据计算甲乙的平均数和方差,再比较即可,
(2)用列举法求出基本事件数,计算出对应的概率即可.
解答 解:(1)甲的平均数是$\overline{{x}_{甲}}$=$\frac{1}{5}$=(87+88+91+91+93)=90,
$\overline{{x}_{乙}}$=$\frac{1}{5}$(85+89+91+92+93)=90,
方差S2甲=$\frac{1}{5}$[(87-90)2+(88-90)2+(91-90)2+(91-90)2+(93-90)2]=$\frac{24}{5}$,
方差S2乙=$\frac{1}{5}$[(85-90)2+(88-90)2+(91-90)2+(92-90)2+(93-90)2]=8,
∴S2甲<S2乙,
∴选甲组参加比赛,
(2)从乙组中抽取2名同学的成绩,所有的基本事件共有10种情况如下:
(85,89),(85,91),(85,92),(85,93),(89,91),
(89,92),(89,93),(91,92),(91,93),(92,93);
则抽取的2名同学的成绩差至少是4分的事件共5种情况如下;
(85,89),(85,91),(85,92),(85,93),(89,93);
故抽取的2名同学的成绩差值至少是4分的概率为P=$\frac{5}{10}$=0.5
点评 本题考查了利用列举法求古典概型的概率问题,也考查了平均数与方差的计算问题,是基础题目.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
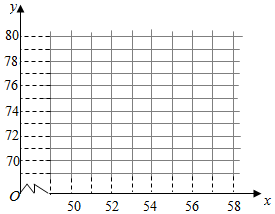 PM2.5是指空气中直径小于或等于2.5微米的颗粒物(也称可入肺颗粒物).为了探究车流量与PM2.5的浓度是否相关,现采集到某城市周一至周五某一时间段车流量与PM2.5的数据如表:
PM2.5是指空气中直径小于或等于2.5微米的颗粒物(也称可入肺颗粒物).为了探究车流量与PM2.5的浓度是否相关,现采集到某城市周一至周五某一时间段车流量与PM2.5的数据如表:| 时间 | 周一 | 周二 | 周三 | 周四 | 周五 |
| 车流量x(万辆) | 50 | 51 | 54 | 57 | 58 |
| PM2.5的浓度y(微克/立方米) | 69 | 70 | 74 | 78 | 79 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{2}$ | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{3}$ | B. | $\frac{11}{3}$ | C. | $\frac{29}{9}$ | D. | $\frac{4}{9}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com