
分析 根据直线Ax+By+C=0的系数A,B,C的特点,对题目中的问题进行分析判断即可.
解答 解:(1)当A•B≠0时,直线Ax+By+C=0化为y=-$\frac{A}{B}$x-$\frac{C}{B}$,与两条坐标轴都相交;
(2)当A≠0且B=0、C≠0时,直线Ax+By+C=0化为x=-$\frac{C}{A}$,只与x轴相交;
(3)当A=0且B≠0、C≠0时,直线Ax+By+C=0化为y=-$\frac{C}{B}$,只与y轴相交;
(4)当A=C=0且B≠0时,直线Ax+By+C=0化为y=0,是x轴所在直线;
(5)当A≠0且B=C=0时,直线Ax+By+C=0化为x=0,是y轴所在直线.
点评 本题考查了直线方程的应用问题,也考查了数形结合思想的应用问题,是基础题目.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 若x∈(-$\frac{π}{2}$,$\frac{π}{2}$),为了运行如图所示的伪代码后输出的y值为-$\frac{\sqrt{3}}{2}$,则应输入的x值为-$\frac{π}{3}$.
若x∈(-$\frac{π}{2}$,$\frac{π}{2}$),为了运行如图所示的伪代码后输出的y值为-$\frac{\sqrt{3}}{2}$,则应输入的x值为-$\frac{π}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
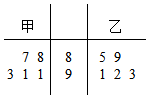 为了参加化学竞赛,某校在甲、乙两个化学特长小组中分别选出5名学生参加比赛,他们取得的成绩(满分100分)的茎叶图如图所示:
为了参加化学竞赛,某校在甲、乙两个化学特长小组中分别选出5名学生参加比赛,他们取得的成绩(满分100分)的茎叶图如图所示:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com