
分析 (1)求出h(x)的导数,得到h(1),h′(1)的值,从而求出切线方程即可;
(2)求出g(x)的导数,得到c=0,得到$\overrightarrow{OP}$•$\overrightarrow{OQ}$=-t2-at2(t-1)ln(-t)<0,所以a(1-t)ln(-t)<1,通过讨论t的范围,从而求出a的范围即可.
解答 解:(1)∵h(x)=(-x3+x2)e1-x,h′(x)=(x3-4x2+2x)e1-x,
∴h(1)=0,h′(1)=-1,
∴h(x)在(1,h(1))处的切线方程为:y=-(x-1),即y=-x+1;
(2)∵g′(x)=$\frac{a}{x}$(x>0),∴g(x)=alnx+c,
∴g(e)=alne+c=a+c=a,得:c=0,从而g(x)=alnx,
设P(t,F(t))为y=F(x)在x≤-1时的图象上的任意一点,则t≤-1,
∵PQ的中点在y轴上,∴Q的坐标为(-t,F(-t)),
∵t≤-1,∴-t≥1,所以P(t,-t3+t2),O(-t,aln(-t)),
∴$\overrightarrow{OP}$•$\overrightarrow{OQ}$=-t2-at2(t-1)ln(-t),由于$\overrightarrow{OP}$•$\overrightarrow{OQ}$<0,所以a(1-t)ln(-t)<1,
当t=-1时,a(1-t)ln(-t)<1恒成立,∴a∈R;
当t<-1时,a<$\frac{1}{(1-t)(ln(-t)}$,令ω(t)=$\frac{1}{(1-t)(ln(-t)}$,(t<-1),
则ω′(t)=$\frac{(t-1)+tln(-t)}{{[(1-t)ln(-t)]}^{2}}$,
∵t<-1,∴t-1<0,tln(-t)<0,∴ω′(t)>0,
从而ω(t)在(-∞,-1)上为增函数,由于t→-∞时,ω(t)→0,ω(t)>0,
∴a≤0.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及函数恒成立问题,是一道综合题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | (-1,2) | C. | (1,3) | D. | (-1,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\sqrt{6}$ | C. | $\frac{{2\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 PM2.5是指空气中直径小于或等于2.5微米的颗粒物(也称可入肺颗粒物).为了探究车流量与PM2.5的浓度是否相关,现采集到某城市周一至周五某一时间段车流量与PM2.5的数据如表:
PM2.5是指空气中直径小于或等于2.5微米的颗粒物(也称可入肺颗粒物).为了探究车流量与PM2.5的浓度是否相关,现采集到某城市周一至周五某一时间段车流量与PM2.5的数据如表:| 时间 | 周一 | 周二 | 周三 | 周四 | 周五 |
| 车流量x(万辆) | 50 | 51 | 54 | 57 | 58 |
| PM2.5的浓度y(微克/立方米) | 69 | 70 | 74 | 78 | 79 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
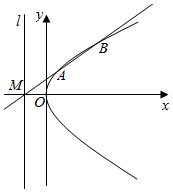 如图,在平面直角坐标系xOy中,抛物线y2=2px(p>0)的准线l与x轴交于点M,过M的直线与抛物线交于A,B两点.设A(x1,y1)到准线l的距离为d,且d=λp(λ>0).
如图,在平面直角坐标系xOy中,抛物线y2=2px(p>0)的准线l与x轴交于点M,过M的直线与抛物线交于A,B两点.设A(x1,y1)到准线l的距离为d,且d=λp(λ>0).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com