
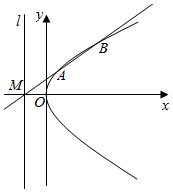
 如图,在平面直角坐标系xOy中,抛物线y2=2px(p>0)的准线l与x轴交于点M,过M的直线与抛物线交于A,B两点.设A(x1,y1)到准线l的距离为d,且d=λp(λ>0).
如图,在平面直角坐标系xOy中,抛物线y2=2px(p>0)的准线l与x轴交于点M,过M的直线与抛物线交于A,B两点.设A(x1,y1)到准线l的距离为d,且d=λp(λ>0).分析 (1)由题意可知x1=1-$\frac{p}{2}$,A点坐标为(1-$\frac{p}{2}$,1),将A点坐标代入抛物线方程求得p的值,写出抛物线的标准方程;
(2)直线AB过M(-$\frac{p}{2}$,0),设直线AB的方程为y=k(x+$\frac{p}{2}$),代入抛物线方程y2=2px,消去y,整理得${k}^{2}{x}^{2}+p({k}^{2}-2)x+\frac{{k}^{2}{p}^{2}}{4}=0$,解出x1、x2,将d=x1+$\frac{p}{2}$,代入d=λp,得${x}_{1}+\frac{p}{2}=λp$,$\overrightarrow{AM}$+λ$\overrightarrow{AB}$=$\overrightarrow{0}$,可知,${x}_{1}+\frac{p}{2}=λ({x}_{2}-{x}_{1})$,将x1、x2代入,即可解得${k}^{2}=2\sqrt{2}-2$,可证直线AB的斜率为定值.
解答 解:(1)由条件知,x1=1-$\frac{p}{2}$,则A点坐标为(1-$\frac{p}{2}$,1),代入抛物线方程得p=1,
∴抛物线方程为y2=2x,
(2)证明:设B(x2,y2),直线AB的方程为y=k(x+$\frac{p}{2}$),
将直线AB的方程代入y2=2px,消去y得:${k}^{2}{x}^{2}+p({k}^{2}-2)x+\frac{{k}^{2}{p}^{2}}{4}=0$,
解得:x1=$\frac{-p({k}^{2}-2)-2p\sqrt{1-{k}^{2}}}{2k}$,x2=$\frac{-p({k}^{2}-2)+2p\sqrt{1-{k}^{2}}}{2{k}^{2}}$.
∵d=λp,
∴${x}_{1}+\frac{p}{2}=λp$,
$\overrightarrow{AM}$+λ$\overrightarrow{AB}$=$\overrightarrow{0}$,${x}_{1}+\frac{p}{2}=λ({x}_{2}-{x}_{1})$,
∴p=x2-x1=$\frac{2p\sqrt{1-{k}^{2}}}{{k}^{2}}$,
∴${k}^{2}=2\sqrt{2}-2$,
∴直线AB的斜率为定值.
点评 本题考查抛物线的方程和性质,以及点到直线的距离公式和综合运用数学知识解决问题的能力,属于中档题.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$f($\frac{π}{3}$)<$\sqrt{2}$f($\frac{π}{4}$)<$\sqrt{3}$f($\frac{π}{4}$)<$\sqrt{3}$f($\frac{π}{3}$) | B. | $\sqrt{2}$f($\frac{π}{4}$)<$\sqrt{2}$f($\frac{π}{3}$)<$\sqrt{3}$f($\frac{π}{3}$)<$\sqrt{3}$f($\frac{π}{4}$) | ||
| C. | $\sqrt{2}$f($\frac{π}{4}$)<$\sqrt{2}$f($\frac{π}{3}$)<$\sqrt{3}$f($\frac{π}{4}$)<$\sqrt{3}$f($\frac{π}{3}$) | D. | $\sqrt{2}$f($\frac{π}{4}$)<$\sqrt{3}$f($\frac{π}{4}$)<$\sqrt{2}$f($\frac{π}{3}$)<$\sqrt{3}$f($\frac{π}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $±\frac{{\sqrt{2}}}{2}$ | B. | $±\frac{{\sqrt{3}}}{2}$ | C. | ±1 | D. | $±\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=-2x | B. | y=3x | C. | y=-3x | D. | y=2x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1)∪(0,1) | B. | (-1,0)∪(1,+∞) | C. | (-∞,-1)∪(-1,0) | D. | (0,1)∪(1,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com