
分析 (Ⅰ)求出函数的导数,求得单调区间,由单调性,即可判断函数的零点个数;
(Ⅱ)(i)求出g(x)的导数,从而判断出g(x)的单调性,(ii)要证x1+x2<3ea-1-1,可知知,p是h(x)的唯一最大值点,故有$\left\{\begin{array}{l}{h(p)>0}\\{{x}_{1}<p{<x}_{2}}\end{array}\right.$,作函数m(x)=lnx-$\frac{2(x-p)}{x+p}$-lnp,通过导数判断单调性,整理,变形,即可得证.
解答 解:(Ⅰ)f′(x)=$\frac{1-x}{{x}^{2}}$,令f′(x)=0,解得:x=1,
当0<x<1时,f′(x)>0,f(x)在(0,1)递增,
当x>1时,f′(x)<0,f(x)在(1,+∞)递减,
f(x)max=f(1)=a-1,
①当f(x)max=0,解得:a=1,此时最大值点唯一,符合题意,
②当f(x)max<0,即a<1时,f(x)<0恒成立,不符合题意,
③当f(x)max>0,即a>1时,ea>1,f(ea)=-$\frac{1}{{e}^{a}}$<0,e-a<1,
∴f(e-a)=2a-ea≤2a-ea<0,(易证ex≥ex),
∴f(x)有2个零点,不符合题意,
综上:a=1;
(Ⅱ)(i)由g(x)=a-$\frac{1}{x}$-$\frac{2(x-p)}{x+p}$-f(x)-lnp,
得:g(x)=lnx-$\frac{2(x-p)}{x+p}$-lnp,
函数g(x)的定义域是(0,+∞),且p>0,
∵g′(x)=$\frac{{(x-p)}^{2}}{{x(x+p)}^{2}}$≥0,
∴g(x)在(0,+∞)单调递增;
(ii)f(x)=0?h(x)=ax-1-xlnx=0,故x1,x2也是h(x)=0的两个零点.
由h′(x)=a-1-lnx=0,得x=ea-1(记p=ea-1).
可知,p是h(x)的唯一最大值点,故有$\left\{\begin{array}{l}{h(p)>0}\\{{x}_{1}<p{<x}_{2}}\end{array}\right.$,
作函数m(x)=lnx-$\frac{2(x-p)}{x+p}$-lnp,则m′(x)=$\frac{{(x-p)}^{2}}{{x(x+p)}^{2}}$≥0,故m(x)单调递增.
当x>p时,h(x)>h(p)=0;当0<x<p时,h(x)<0.
于是,ax1-1=x1lnx1<$\frac{{2x}_{1}{(x}_{1}-p)}{{x}_{1}+p}$+x1lnp.
整理,得(2+lnp-a)x12-(2p+ap-plnp-1)x1+p>0,
即x12-(3ea-1-1)x1+ea-1>0.
同理x22-(3ea-1-1)x2+ea-1<0.
故x22-(3ea-1-1)x2+ea-1<x12-(3ea-1-1)x1+ea-1,
即(x2+x1)(x2-x1)<(3ea-1-1)(x2-x1),
于是x1+x2<3ea-1-1.
点评 本题考查函数的性质和运用,主要考查函数的零点的求法和取值范围,同时考查导数的运用:求单调区间和极值、最值,运用构造函数判断单调性是解题的关键.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\sqrt{6}$ | C. | $\frac{{2\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
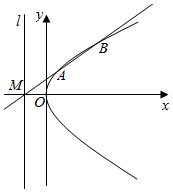 如图,在平面直角坐标系xOy中,抛物线y2=2px(p>0)的准线l与x轴交于点M,过M的直线与抛物线交于A,B两点.设A(x1,y1)到准线l的距离为d,且d=λp(λ>0).
如图,在平面直角坐标系xOy中,抛物线y2=2px(p>0)的准线l与x轴交于点M,过M的直线与抛物线交于A,B两点.设A(x1,y1)到准线l的距离为d,且d=λp(λ>0).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既非充分又非必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com