

| A. | 4 | B. | 5 | C. | 6 | D. | 3 |
分析 模拟执行程序框图,依次得到s,n的值,当S=$\frac{3}{2}$时,由题意不满足条件,退出循环,输出n的值为3,从而得解.
解答 解:程序运行过程为:开始→p=$\frac{11}{12}$→n=1,S=0→S<p成立,
执行循环体,S=0+$\frac{1}{2}$×1=$\frac{1}{2}$,n=1+1=2→S<p仍成立,
执行循环体,S=$\frac{1}{2}$+$\frac{1}{2}$×2=$\frac{3}{2}$,n=2+1=3→S<p不成立,
输出n的值3后结束,
故选:D.
点评 本题考查循环结构,解答本题,关键是根据框图得出算法,计算出循环次数,再由S的变化规律得出退出循环的条件,本题是框图考查常见的形式,较多见,题后作好总结,属于基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
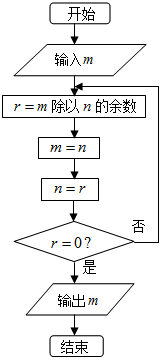 如图程序框图的算法思路源于我国古代数学名著《九章算术》中的某一种算法.执行该程序框图,输入分别为98,63,则输出的结果是( )
如图程序框图的算法思路源于我国古代数学名著《九章算术》中的某一种算法.执行该程序框图,输入分别为98,63,则输出的结果是( )| A. | 14 | B. | 18 | C. | 9 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1)∪(0,1) | B. | (-1,0)∪(1,+∞) | C. | (-∞,-1)∪(-1,0) | D. | (0,1)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 2 | C. | $\sqrt{3}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a1a2>0,则a2a3>0 | B. | 若a1a3<0,则a1a2<0 | ||
| C. | 若a1<a2,则a22<a1a3 | D. | 若a1≥a2,则a22≥a1a3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com