Question

已知函数f（x）=bx，g（x）=ax²+1，h（x）=ln（1+x²）．（a，b∈R）
（1）若M={x|f（x）+g（x）≥0}，-1∈M，2∈M，z=3a-b，求z的取值范围；
（2）设F（x）=f（x）+h（x），且b≤0，试讨论函数F（x）的单调性．

Answer 1

分析：（1）原不等式f（x）+g（x）≥0即ax²+bx+1≥0，由-1∈M，2∈M得

a-b+1≥0 4a+2b+1≥0

画出不等式组所确定的可行域，利用线性规划的方法即可求得z的取值范围；
（2）对F（x）求导数得F/(x)=

2x

1+x2

+b=

bx2+2x+b

1+x2

，下面对字母b进行分类讨论：当b=0时，F（x）在（0，+∞）单调递增，在（-∞，0）单调递减；当b＜0时，F（x）在（-∞，+∞）上单调递减；当-1＜b＜0时，讨论函数F（x）的单调性即可．

解答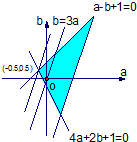：解：（1）解：不等式f（x）+g（x）≥0即ax²+bx+1≥0
由-1∈M，2∈M得

a-b+1≥0 4a+2b+1≥0

----------------（2分）
画出不等式组所确定的可行域如右图示：作平行线族b=3a-z
可见当a=-0.5，b=0.5时z有最小值，，z_min=-2--------------------（5分）
∴z的取值范围为z≥-2．----------------------------------------（6分）
（2）∵F（x）=bx+ln（1+x²）
∴F/(x)=

2x

1+x2

+b=

bx2+2x+b

1+x2

----------------（8分）
当b=0时，F/(x)=

2x

1+x2

＞0?x＞0
∴F（x）在（0，+∞）单调递增，在（-∞，0）单调递减；-----------------（9分）
当b＜0时，由bx²+2x+b=0的判别式△=4-4b²=0，得b=-1∴F′（x）≤0
当b≤-1时，对x∈R恒成立
∴F（x）在（-∞，+∞）上单调递减；-----------------------（10分）
当-1＜b＜0时，由F′（x）＞0得：bx²+2x+b＞0
解得：

-1+ 1-b2

b

＜x＜

-1- 1-b2

b

由F′（x）＜0可得：x＞

-1- 1-b2

b

或x＜

-1+ 1-b2

b

-----------------------（12分）
∴当-1＜b＜0时F（x）在(

-1+ 1-b2

b

，

-1- 1-b2

b

)上单调递增，
在(-∞，

-1+ 1-b2

b

)和(

-1- 1-b2

b

，+∞)上单调递减．-------------------（14分）

点评：本小题主要考查利用导数研究函数的单调性、简单线性规划的应用、不等式的解法等基础知识，考查运算求解能力，考查数形结合思想、化归与转化思想．属于基础题．