
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD为正方形,PA⊥底面ABCD,AD=AP,E为棱PD中点. 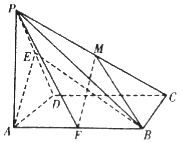
(1)求证:PD⊥平面ABE;
(2)若F为AB中点, ![]() ,试确定λ的值,使二面角P﹣FM﹣B的余弦值为-
,试确定λ的值,使二面角P﹣FM﹣B的余弦值为- ![]() .
.
【答案】
(1)证明:∵PA⊥底面ABCD,AB底面ABCD,∴PA⊥AB,
又∵底面ABCD为矩形,∴AB⊥AD,PA∩AD=A,PA平面PAD,AD平面PAD,
∴AB⊥平面PAD,又PD平面PAD,∴AB⊥PD,AD=AP,E为PD中点,∴AE⊥PD,AE∩AB=A,AE平面ABE,AB平面ABE,∴PD⊥平面ABE
(2)以A为原点,以 ![]() 为x,y,z轴正方向,建立空间直角坐标系A﹣BDP,令|AB|=2,
为x,y,z轴正方向,建立空间直角坐标系A﹣BDP,令|AB|=2,

则A(0,0,0),B(2,0,0),P(0,0,2),C(2,2,0),E(0,1,1),F(1,0,0), ![]() ,
, ![]() ,
, ![]() ,M(2λ,2λ,2﹣2λ)
,M(2λ,2λ,2﹣2λ)
设平面PFM的法向量 ![]() ,
, 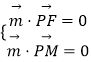 ,即
,即 ![]() ,
, ![]()
设平面BFM的法向量 ![]() ,
, 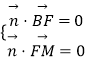 ,
,
即 ![]() ,
, ![]()
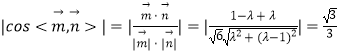 ,解得
,解得 ![]()
【解析】(I)证明AB⊥平面PAD,推出AB⊥PD,AE⊥PD,AE∩AB=A,即可证明PD⊥平面ABE.(II) 以A为原点,以 ![]() 为x,y,z轴正方向,建立空间直角坐标系A﹣BDP,求出相关点的坐标,平面PFM的法向量,平面BFM的法向量,利用空间向量的数量积求解即可.
为x,y,z轴正方向,建立空间直角坐标系A﹣BDP,求出相关点的坐标,平面PFM的法向量,平面BFM的法向量,利用空间向量的数量积求解即可.


科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象与
的图象与![]() 轴的交点中相邻两个交点的距离是
轴的交点中相邻两个交点的距离是![]() ,当
,当![]() 时
时![]() 取得最小值
取得最小值![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)求函数![]() 在区间
在区间![]() 的最大值和最小值;
的最大值和最小值;
(3)若函数![]() 的零点为
的零点为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角梯形![]() 中,
中, ![]() ,
, ![]() 为线段
为线段![]() (含端点)上一个动点,设
(含端点)上一个动点,设![]() 对于函数
对于函数![]() ,给出以下三个结论:
,给出以下三个结论:
①当![]() 时,函数
时,函数![]() 的值域为
的值域为![]() ;
;
②对于任意的![]() ,均有
,均有![]() ;
;
③对于任意的![]() ,函数
,函数![]() 的最大值均为4.
的最大值均为4.
其中所有正确的结论序号为__________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列{an}满足(1﹣a1008)5+2016(1﹣a1008)=1,(1﹣a1009)5+2016(1﹣a1009)=﹣1,数列{an}的前n项和记为Sn , 则( )
A.S2016=2016,a1008>a1009
B.S2016=﹣2016,a1008>a1009
C.S2016=2016,a1008<a1009
D.S2016=﹣2016,a1008<a1009
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足
满足![]() ,且
,且![]() .
.
(Ⅰ)证明:数列![]() 为等差数列,并求数列
为等差数列,并求数列![]() 的通项公式;
的通项公式;
(Ⅱ)若记![]() 为满足不等式
为满足不等式![]() 的正整数
的正整数![]() 的个数,设
的个数,设![]() ,求数列
,求数列![]() 的最大项与最小项的值.
的最大项与最小项的值.
【答案】(1)见解析;(2)最大项为![]() ,最小项为
,最小项为![]() .
.
【解析】试题分析:(Ⅰ)对![]() 两边取倒数,移项即可得出
两边取倒数,移项即可得出![]() ,故而数列
,故而数列![]() 为等差数列,利用等差数列的通项公式求出
为等差数列,利用等差数列的通项公式求出![]() ,从而可得出
,从而可得出![]() ;(Ⅱ)根据不等式
;(Ⅱ)根据不等式![]() ,,得
,,得![]() ,又
,又![]() ,从而
,从而![]() ,当
,当![]() 为奇数时,
为奇数时,![]() 单调递减,
单调递减,![]() ;当
;当![]() 为偶数时
为偶数时![]() 单调递增,
单调递增,![]() 综上
综上![]() 的最大项为
的最大项为![]() ,最小项为
,最小项为![]() .
.
试题解析:(Ⅰ)由于![]() ,
,![]() ,则
,则![]()
∴![]() ,则
,则![]() ,即
,即![]() 为常数
为常数
又![]() ,∴数列
,∴数列![]() 是以1为首项,
是以1为首项,![]() 为公比的等比数列
为公比的等比数列
从而![]() ,即
,即![]() .
.
(Ⅱ)由![]() 即
即![]() ,得
,得![]() ,
,
又![]() ,从而
,从而![]()
故
当![]() 为奇数时,
为奇数时, ,
,![]() 单调递减,
单调递减,![]() ;
;
当![]() 为偶数时,
为偶数时, ,
,![]() 单调递增,
单调递增,![]()
综上![]() 的最大项为
的最大项为![]() ,最小项为
,最小项为![]() .
.
【题型】解答题
【结束】
22
【题目】已知向量![]() ,
,![]()
![]() ,若函数
,若函数![]() 的最小正周期为
的最小正周期为![]() ,且在区间
,且在区间![]() 上单调递减.
上单调递减.
(Ⅰ)求![]() 的解析式;
的解析式;
(Ⅱ)若关于![]() 的方程
的方程![]() 在
在![]() 有实数解,求
有实数解,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(x﹣2)ex+a(x+2)2(x>0).
(1)若f(x)是(0,+∞)的单调递增函数,求实数a的取值范围;
(2)当 ![]() 时,求证:函数f(x)有最小值,并求函数f(x)最小值的取值范围.
时,求证:函数f(x)有最小值,并求函数f(x)最小值的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在平面直角坐标系xOy中,以坐标原点O为极点,以x轴正半轴为极轴,建立极坐标系,曲线C1的极坐标方程为ρ=4cosθ,直线l的参数方程为 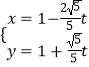 (t为参数).
(t为参数).
(1)求曲线C1的直角坐标方程及直线l的普通方程;
(2)若曲线C2的参数方程为 ![]() (α为参数),曲线C1上点P的极角为
(α为参数),曲线C1上点P的极角为 ![]() ,Q为曲线C2上的动点,求PQ的中点M到直线l距离的最大值.
,Q为曲线C2上的动点,求PQ的中点M到直线l距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年,在国家创新驱动战略下,北斗系统作为一项国家高科技工程,一个开放型的创新平台,1400多个北斗基站遍布全国,上万台设备组成星地“一张网”,国内定位精度全部达到亚米级,部分地区达到分米级,最高精度甚至可以达到厘米或毫米级。最近北斗三号工程耗资![]() 元建成一大型设备,已知这台设备维修和消耗费用第一年为
元建成一大型设备,已知这台设备维修和消耗费用第一年为![]() 元,以后每年增加
元,以后每年增加![]() 元(
元(![]() 是常数),用
是常数),用![]() 表示设备使用的年数,记设备年平均维修和消耗费用为
表示设备使用的年数,记设备年平均维修和消耗费用为![]() ,即
,即![]() (设备单价
(设备单价![]() 设备维修和消耗费用)
设备维修和消耗费用)![]() 设备使用的年数.
设备使用的年数.
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)当![]() ,
, ![]() 时,求这种设备的最佳更新年限.
时,求这种设备的最佳更新年限.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线C1 ![]() (t为参数),C2
(t为参数),C2 ![]() (θ为参数),
(θ为参数),
(Ⅰ)当α= ![]() 时,求C1与C2的交点坐标;
时,求C1与C2的交点坐标;
(Ⅱ)过坐标原点O做C1的垂线,垂足为A,P为OA中点,当α变化时,求P点的轨迹的参数方程,并指出它是什么曲线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com