
����Ŀ��2017�꣬�ڹ��Ҵ�������ս���£�����ϵͳ��Ϊһ����Ҹ߿Ƽ����̣�һ�������͵Ĵ���ƽ̨��1400���������վ�鲼ȫ��������̨�豸����ǵء�һ�����������ڶ�λ����ȫ���ﵽ���������ֵ����ﵽ��������߾����������Դﵽ�������������������Ź��̺���![]() Ԫ����һ�����豸����֪��̨�豸ά�����ķ��õ�һ��Ϊ
Ԫ����һ�����豸����֪��̨�豸ά�����ķ��õ�һ��Ϊ![]() Ԫ���Ժ�ÿ������
Ԫ���Ժ�ÿ������![]() Ԫ��
Ԫ��![]() �dz���������
�dz���������![]() ��ʾ�豸ʹ�õ����������豸��ƽ��ά�����ķ���Ϊ
��ʾ�豸ʹ�õ����������豸��ƽ��ά�����ķ���Ϊ![]() ����
����![]() (�豸����
(�豸����![]() �豸ά�����ķ��ã�
�豸ά�����ķ��ã�![]() �豸ʹ�õ�������
�豸ʹ�õ�������
��1����![]() ����
����![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
��2����![]() ��
�� ![]() ʱ���������豸����Ѹ������ޣ�
ʱ���������豸����Ѹ������ޣ�
���𰸡�(1) ![]() ;(2) �����豸����Ѹ�������Ϊ15�꣮
;(2) �����豸����Ѹ�������Ϊ15�꣮
�������������������1�������⣬����ÿ���ά�����ķ���Ϊ�Ȳ����У��ɸ��ݵȲ�����ǰ![]() ���ʽ����
���ʽ����![]() ���Ӷ�����ɵý⣻��2�������⣬��
���Ӷ�����ɵý⣻��2�������⣬��![]() ��ֵ���루1���Ĺ�ϵʽ���õ�
��ֵ���루1���Ĺ�ϵʽ���õ�![]() ����
����![]() �ĺ�����ϵ�����ɻ�������ʽ�������ֵ���Ӷ�������ڽ��.
�ĺ�����ϵ�����ɻ�������ʽ�������ֵ���Ӷ�������ڽ��.
���������(1)�����⣬�豸ά�����ķ��ù�����![]() Ϊ���
Ϊ���![]() Ϊ����ĵȲ����У�
Ϊ����ĵȲ����У�
�����ƽ��ά�����ķ���Ϊ![]()
������![]()
(2)�ɣ�1����֪����![]() ��
�� ![]() ʱ��
ʱ��
![]()
![]()
���ҽ���![]()
�������豸����Ѹ�������Ϊ15�꣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() ���㣺�ڶ�����
���㣺�ڶ�����![]() �ڴ���ʵ��
�ڴ���ʵ��![]() ��ʹ��
��ʹ��![]() ��������ƺ���
��������ƺ���![]() Ϊ��
Ϊ��![]() �ı��ͺ�����.���������ĸ���������
�ı��ͺ�����.���������ĸ���������![]() ����
����![]() �� ��
�� ��![]() ����
����![]() .�����ǡ�
.�����ǡ�![]() �ı��ͺ����������к����������______________.
�ı��ͺ����������к����������______________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������P��ABCD�У�����ABCDΪ�����Σ�PA�͵���ABCD��AD=AP��EΪ��PD�е㣮 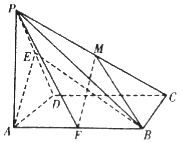
��1����֤��PD��ƽ��ABE��
��2����FΪAB�е㣬 ![]() ����ȷ���˵�ֵ��ʹ�����P��FM��B������ֵΪ-
����ȷ���˵�ֵ��ʹ�����P��FM��B������ֵΪ- ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����{an}����an+1��an=2��a1=��5����|a1|+|a2|+��+|a6|=�� ��
A.9
B.15
C.18
D.30
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����a>0��a��1������f(x)��![]() x2��(a��1)x��alnx.
x2��(a��1)x��alnx.
(1)��a��2ʱ��������y��f(x)��(3��f(3))�����ߵ�б�ʣ�
(2)����f(x)�ļ�ֵ�㣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=��x��2��ex+a��x+2��2��x��0����
��1����f��x���ǣ�0��+�ޣ��ĵ���������������ʵ��a��ȡֵ��Χ��
��2���� ![]() ʱ����֤������f��x������Сֵ��������f��x����Сֵ��ȡֵ��Χ��
ʱ����֤������f��x������Сֵ��������f��x����Сֵ��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯�� ![]() ��
�� ![]() Ϊ������e=2.71828��������Ȼ�����ĵ�������
Ϊ������e=2.71828��������Ȼ�����ĵ�������
��1���� ![]() ʱ������
ʱ������ ![]() �ĵ������䣻
�ĵ������䣻
��2�������� ![]() ��
�� ![]() �ڴ���������ֵ�㣬��
�ڴ���������ֵ�㣬�� ![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��һϵ�ж�Ӧֵ���±���
��һϵ�ж�Ӧֵ���±���
|
|
|
|
|
|
|
|
| -1 | 1 | 3 | 1 | -1 | 1 | 3 |
��1�����ݱ����ṩ�����ݻ�������![]() ��ͼ�������������ʽ��
��ͼ�������������ʽ��
��2������(1)�Ľ����������![]() ������Ϊ
������Ϊ![]() ����
����![]() ʱ������
ʱ������![]() ǡ��������ͬ�Ľ⣬��ʵ��
ǡ��������ͬ�Ľ⣬��ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����{an}�У�a1=1��a3=9����an=an��1+��n��1��n��2����
��1����˵�ֵ������{an}��ͨ�ʽ��
��2���� ![]() ��������{bn}��ǰn���ΪSn �� ��S2n ��
��������{bn}��ǰn���ΪSn �� ��S2n ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com