
已知函数f(x)=4cos ωx· (ω>0)的最小正周期为π.
(ω>0)的最小正周期为π.
(1)求ω的值;
(2)讨论f(x)在区间 上的单调性.
上的单调性.
(1)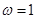 (2)
(2) 在
在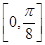 单调递增,在
单调递增,在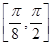 单调递减.
单调递减.
解析试题分析:(1)利用两角和正弦公式和降幂公式化简,得到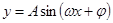 的形式,利用公式
的形式,利用公式 计算周期.(2)利用正弦函数的单调区间,求在
计算周期.(2)利用正弦函数的单调区间,求在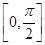 的单调性.(3)求三角函数的最小正周期一般化成
的单调性.(3)求三角函数的最小正周期一般化成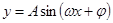 ,
, ,
, 形式,利用周期公式即可.(4)求解较复杂三角函数的单调区间时,首先化成
形式,利用周期公式即可.(4)求解较复杂三角函数的单调区间时,首先化成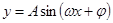 形式,再
形式,再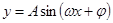 的单调区间,只需把
的单调区间,只需把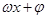 看作一个整体代入
看作一个整体代入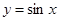 相应的单调区间,注意先把
相应的单调区间,注意先把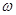 化为正数,这是容易出错的地方.
化为正数,这是容易出错的地方.
试题解析:解:(1)f(x)=4cos ωx·sin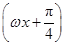
=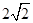 sin ωx·cos ωx+
sin ωx·cos ωx+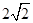 cos2ωx
cos2ωx
=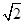 (sin 2ωx+cos 2ωx)+
(sin 2ωx+cos 2ωx)+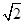
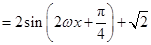 3分
3分
因为f(x)的最小正周期为π,且ω>0,
从而有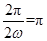 ,故ω=1. 6分
,故ω=1. 6分
(2)由(1)知,f(x)=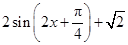 .
.
若0≤x≤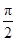 ,则
,则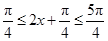 .
.
当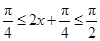 ,即
,即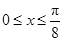 时,f(x)单调递增;
时,f(x)单调递增;
当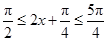 ,即
,即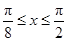 时,f(x)单调递减. 10分
时,f(x)单调递减. 10分
综上可知,f(x)在区间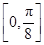 上单调递增,在区间
上单调递增,在区间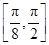 上单调递减. 12分
上单调递减. 12分
考点:(1)利用公式对三角函数进行化简.(2)求正弦型函数的单调区间.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com