
已知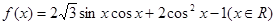
(1)求函数 的最小正周期及在区间
的最小正周期及在区间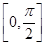 上的最大值和最小值;
上的最大值和最小值;
(2)若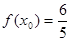 ,
,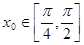 ,求
,求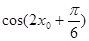 的值.
的值.
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:高中数学 来源: 题型:解答题
函数f(x)=Asin(wx+j)(A>0,w>0,- <j<
<j< ,x∈R)的部分图象如图所示:
,x∈R)的部分图象如图所示: ,
,
(1)求函数y=f(x)的解析式;(2)当x∈ 时,求f(x)的取值范围.
时,求f(x)的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
受日月引力影响,海水会发生涨退潮现象.通常情况下,船在涨潮时驶进港口,退潮时离开港口.某港口在某季节每天港口水位的深度 (米)是时间
(米)是时间 (
( ,单位:小时,
,单位:小时, 表示0:00—零时)的函数,其函数关系式为
表示0:00—零时)的函数,其函数关系式为

 .已知一天中该港口水位的深度变化有如下规律:出现相邻两次最高水位的深度的时间差为12小时,最高水位的深度为12米,最低水位的深度为6米,每天13:00时港口水位的深度恰为10.5米.
.已知一天中该港口水位的深度变化有如下规律:出现相邻两次最高水位的深度的时间差为12小时,最高水位的深度为12米,最低水位的深度为6米,每天13:00时港口水位的深度恰为10.5米.
(1)试求函数 的表达式;
的表达式;
(2)某货船的吃水深度(船底与水面的距离)为7米,安全条例规定船舶航行时船底与海底的距离不小于3.5米是安全的,问该船在当天的什么时间段能够安全进港?若该船欲于当天安全离港,则它最迟应在当天几点以前离开港口?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com