解:(1)直线l'∥l,
可设l':2x+y+m=0
∵l'被圆C截得的弦长为

,
故圆C:x
2+y
2=4的圆心(0,0)到l'的距离d与半弦长

=

及半径r=2构成直角三角形,满足勾股定理
即d
2=r
2-(

)
2=4-3=1,即d=1
又∵弦心距d=

∴1=

解得m=±

即l'的方程为:2x+y

=0
(2)∵PT与圆切于P点
∴CT
2=PT
2+CP
2=25
设T点坐标为(x,y)则

解得

或
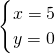
即T点坐标为(3,4)或(5,0)
(3)存在(1,1)点为B点时,满足
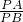
为定值

>1满足要求,
理由如下:
P点到A(2,2)的距离平方为(x-2)
2+(y-2)
2=x
2+y
2-4x-4y+8=12-4x-4y
P点到B(1,1)的距离平方为(x-1)
2+(y-1)
2=x
2+y
2-2x-2y+2=6-2x-2y
即

=

=2
故
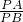
=

>1
分析:(1)根据平行直线的直线系方程,我们设出直线l'的方程,进而根据圆C:x
2+y
2=4的圆心(0,0)到l'的距离d与半弦长

=

及半径r=2构成直角三角形,满足勾股定理,求出圆心到直线的距离,进而由点到直线距离公式,构造关于m的方程,解方程即可求出直线l'的方程;
(2)根据过点P作圆C的切线,设此切线交直线l于点T,且
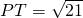
,我们可得CT
2=25,T点坐标为(x,y)根据两点之间距离公式,即可求出点T的坐标;
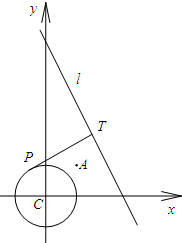
(3)存在(1,1)点为B点时,满足
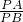
为定值

>1,由两点间距离公式,结合P点在圆上满足x
2+y
2=4,易证得结论.
点评:本题考查的知识点是直线与圆的方程及应用,直线与圆相交的性质,直线与圆相切的性质,点到点的距离公式,点到直线的距离公式,其中(1)的关键是圆C:x
2+y
2=4的圆心(0,0)到l'的距离d与半弦长

=

及半径r=2构成直角三角形,满足勾股定理;(2)的关键是根据已知求出CT
2=25,(3)的关键是求出B点坐标.

 在平面直角坐标系xOy中,已知圆C:x2+y2=4和直线l:2x+y-10=0,点P为圆C上任意一点.
在平面直角坐标系xOy中,已知圆C:x2+y2=4和直线l:2x+y-10=0,点P为圆C上任意一点. ,求直线l'的方程;
,求直线l'的方程;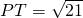 ,求点T的坐标;
,求点T的坐标;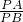 为定值k(k>1)?请证明你的结论.
为定值k(k>1)?请证明你的结论. ,
, =
= 及半径r=2构成直角三角形,满足勾股定理
及半径r=2构成直角三角形,满足勾股定理 )2=4-3=1,即d=1
)2=4-3=1,即d=1


 =0
=0
 或
或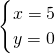
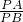 为定值
为定值 >1满足要求,
>1满足要求, =
= =2
=2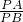 =
= >1
>1 =
= 及半径r=2构成直角三角形,满足勾股定理,求出圆心到直线的距离,进而由点到直线距离公式,构造关于m的方程,解方程即可求出直线l'的方程;
及半径r=2构成直角三角形,满足勾股定理,求出圆心到直线的距离,进而由点到直线距离公式,构造关于m的方程,解方程即可求出直线l'的方程;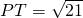 ,我们可得CT2=25,T点坐标为(x,y)根据两点之间距离公式,即可求出点T的坐标;
,我们可得CT2=25,T点坐标为(x,y)根据两点之间距离公式,即可求出点T的坐标;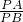 为定值
为定值 >1,由两点间距离公式,结合P点在圆上满足x2+y2=4,易证得结论.
>1,由两点间距离公式,结合P点在圆上满足x2+y2=4,易证得结论. =
= 及半径r=2构成直角三角形,满足勾股定理;(2)的关键是根据已知求出CT2=25,(3)的关键是求出B点坐标.
及半径r=2构成直角三角形,满足勾股定理;(2)的关键是根据已知求出CT2=25,(3)的关键是求出B点坐标. 

 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.
如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.