练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    2．班级内五名同学参加三个比赛项目，要求每个项目至少一人参加，则共有多少种不同方法（　　）
    A．1080B．540C．180D．150

    分析 由题意知5名同学被安排参加三个不同的工作每个项目至少有一人参加，可以把5个人分成三组，一种是按照1、1、3；另一种是1、2、2；当按照1、1、3来分时共有C53A33，当按照1、2、2来分时注意其中包含一个平均分组的问题，不要出错．

    解答 解：∵5名同学被安排参加三个不同的工作每个项目至少有一人参加，
    ∴可以把5个人分成三组，
    一种是按照1、1、3；另一种是1、2、2
    当按照1、1、3来分时共有C53A33=60，
    当按照1、2、2来分时共有$\frac{{C}_{5}^{2}{C}_{3}^{2}{A}_{3}^{3}}{{A}_{2}^{2}}$=90，
    根据分类计数原理知共有60+90=150，
    故选D．

    点评 本题考查排列组合与分类计数原理，是一个基础题，对于复杂一点的计数问题，有时分类以后，每类方法并不都是一步完成的，必须在分类后又分步，综合利用两个原理解决．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    12．若$\left\{{\begin{array}{l}{y≤1}\\{y≥|x|}\end{array}}\right.$，则x+3y的最大值是4．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．已知函数f（x）=sin（ωx+φ）（ω＞0，|φ|＜π的部分图象如图所示：
    （1）求ω，φ的值；
    （2）求f（x）的单调递增区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．函数y=x3-2x2+1在区间[-1，2]上的最大与最小值为（　　）
    A．2，-1B．2，1C．-1，-2D．1，-2

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．求下列各式的值：
    （1）36${\;}^{\frac{1}{2}}$；
    （2）（$\frac{1}{27}$）${\;}^{\frac{2}{3}}$；
    （3）10000${\;}^{\frac{1}{4}}$；
    （4）（$\frac{16}{49}$）${\;}^{-\frac{1}{2}}$；
    （5）4${\;}^{-\frac{3}{2}}$；
    （6）（6$\frac{1}{4}$）${\;}^{\frac{3}{2}}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．在正四面体S-ABC中，若点E、F分别为SC、AB的中点，则异面直线EF、SA的夹角大小为45°．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

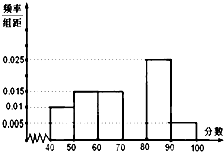    14．某校高二年级共1000人，从参加期末数学考试的学生中抽出20名学生，将其成绩（均为整数）分成六段[40，50），[50，60）…[90，100]，然后画出如图所示频率分布直方图，但是缺失了第四组[70，80）的信息．观察图形的信息，回答下列问题．
    （1）求第四组[70，80）的频率；并估计该年级分数在该段的人数．
    （2）估计该年级这次数学考试的平均数．
    （3）在样本中，从成绩是[50，60）和[60，70）的两段学生中任意选两人，求他们在同一分数段的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．已知f：N*→N*是从N*到N*的增函数，且f（1）=2，f[f（k）]=3k，则f（5）=8．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    12．对定义域分别为D1，D2的函数y=f（x），y=g（x），规定：函数h（x）=$\left\{\begin{array}{l}{f（x）•g（x），x∈{D}_{1}且x∈{D}_{2}}\\{f（x），x∈{D}_{1}且x∉{D}_{2}}\\{g（x），x∉{D}_{1}且x∈{D}_{2}}\end{array}\right.$，f（x）=x-2（x≥1），g（x）=-2x+3（x≤2），则h（x）的单调减区间是（-∞，1），[$\frac{7}{4}$，2]．

    查看答案和解析>>

    同步练习册答案