
已知△ABC中,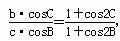 试判断△ABC的形状.
试判断△ABC的形状.
科目:高中数学 来源: 题型:
我国是一个人口大国,随着时间推移,老龄化现象越来越严重,为缓解社会和家庭压力,决定采用养老储备金制度.公民在就业的第一年交纳养老储备金,数目为a1,以后每年交纳的数目均比上一年增加d(d>0),因此,历年所交纳的储备金数目a1,a2,…,an是一个公差为d 的等差数列.与此同时,国家给予优惠的计息政策,不仅采用固定利率,而且计算复利.这就是说,如果固定利率为r(r>0),那么,在第n年末,第一年所交纳的储备金就变为a1(1+r)n-1,第二年所交纳的储备金就变为a2(1+r)n-2,…,以Tn表示到第n年所累计的储备金总额.
(1) 写出Tn与Tn-1(n≥2)的递推关系式;
(2) 求证:Tn=An+Bn,其中{An}是一个等比数列,{Bn}是一个等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
设不等式组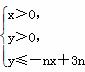 所表示的平面区域为Dn,记Dn内的整点个数为an(n∈N*)(整点即横坐标和纵坐标均为整数的点).
所表示的平面区域为Dn,记Dn内的整点个数为an(n∈N*)(整点即横坐标和纵坐标均为整数的点).
(1) 求数列{an}的通项公式;
(2) 记数列{an}的前n项和为Sn,且Tn=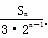 .若对于一切的正整数n,总有Tn≤m,求实数m的取值范围.
.若对于一切的正整数n,总有Tn≤m,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
江岸边有一炮台高30 m,江中有两条船,船与炮台底部在同一水面上,由炮台顶部测得俯角分别为45°和60°,而且两条船与炮台底部连线成30°角,则两条船相距________m.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,半圆O的直径为2,A为直径延长线上的一点,OA=2,B为半圆上任意一点,以AB为一边作等边三角形ABC.问:点B在什么位置时,四边形OACB面积最大?
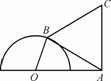
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com