练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

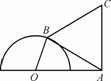
     如图，半圆O的直径为2，A为直径延长线上的一点，OA＝2，B为半圆上任意一点，以AB为一边作等边三角形ABC.问：点B在什么位置时，四边形OACB面积最大？


    解：设∠AOB＝α，在△AOB中，由余弦定理得AB2＝OA2＋OB2－2×OA×OBcos∠AOB＝12＋22－2×1×2×cosα

    ＝5－4cosα，

    于是，四边形OACB的面积为

    四边形OACB面积最大．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    某住宅小区计划植树不少于100棵，若第一天植2棵，以后每天植树的棵树是前一天的2倍，则需要的最少天数n(n∈N*)为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知△ABC中，试判断△ABC的形状．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设A、B两点在河的两岸，一测量者在A所在的河岸边选定一点C，测出AC的距离为50m，∠ACB＝45°，∠CAB＝105°，求A、B两点的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    一人在海面某处测得某山顶C的仰角为α(0°＜α＜45°)，在海面上向山顶的方向行进m m后，测得山顶C的仰角为90°－α，则该山的高度为________m．(结果化简)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在△ABC中，AC＝，BC＝2，B＝60°，则边BC上的高为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知向量m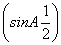＝与n＝(3，sinA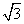＋cosA)共线，其中A是△ABC的内角．

    (1) 求角A的大小；

    (2) 若BC＝2，求△ABC面积S的最大值，并判断S取得最大值时△ABC的形状．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    计算：sin50°(1＋tan10°)．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    　在△ABC中，A(1，－1)，B(1，1)，C(3，－1)，求三边所在直线的倾斜角和斜率．

    查看答案和解析>>

    同步练习册答案