
分析 由g(x)=4f(x)-1=0,得f(x)=$\frac{1}{4}$,作出函数f(x)的表达式,利用数形结合即可得到结论.
解答 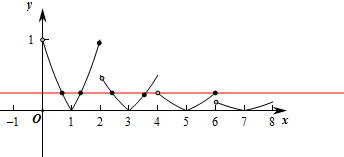 解:由g(x)=4f(x)-1=0,得f(x)=$\frac{1}{4}$,
解:由g(x)=4f(x)-1=0,得f(x)=$\frac{1}{4}$,
要判断函数g(x)的零点个数,则根据f(x)是定义在(-∞,0)∪(0,+∞)上的偶函数,
只需要判断当x>0时f(x)=$\frac{1}{4}$的个数即可,
当0<x≤2时,f(x)=2|x-1|-1∈[0,1],
当2<x≤4时,0<x-2≤2时,f(x)=$\frac{1}{2}$f(x-2)=$\frac{1}{2}$[2|x-3|-1]∈[0,$\frac{1}{2}$],
当4<x≤6时,2<x-2≤4时,f(x)=$\frac{1}{2}$f(x-2)=$\frac{1}{4}$[2|x-5|-1]∈[0,$\frac{1}{4}$],
当6<x≤8时,4<x-2≤6时,f(x)=$\frac{1}{2}$f(x-2)=$\frac{1}{8}$[2|x-7|-1]∈[0,$\frac{1}{8}$],
作出函数f(x)在(0,8)上的图象,由图象可知f(x)=$\frac{1}{4}$有5个根,
则根据偶函数的对称性可知f(x)=$\frac{1}{4}$在定义域(-∞,0)∪(0,+∞)上共有10个根,
即函数g(x)=4f(x)-1的零点个数为10个,
故答案为:10.
点评 本题主要考查函数零点的个数判断,利用函数和方程之间的关系转化为两个函数的交点个数问题,利用分段函数的表达式,作出函数f(x)的图象是解决本题的关键.综合性较强,难度较大.


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:高中数学 来源: 题型:选择题
| A. | ${a_n}={(\frac{3}{2})^{n-1}}$ | B. | ${a_n}=3×{(\frac{1}{2})^{n-1}}$ | C. | an=3n-2 | D. | ${a_n}={3^{n-1}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
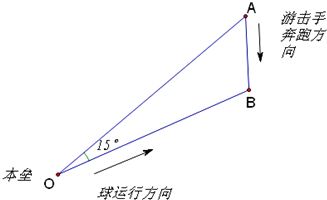 在奥运会垒球比赛前,C国教练布置战术时,要求击球手以与连结本垒及游击手的直线成15°的方向把球击出,根据经验及测速仪的显示,通常情况下球速为游击手最大跑速的4倍,问按这样的布置,游击手能不能接着球?(如图所示)
在奥运会垒球比赛前,C国教练布置战术时,要求击球手以与连结本垒及游击手的直线成15°的方向把球击出,根据经验及测速仪的显示,通常情况下球速为游击手最大跑速的4倍,问按这样的布置,游击手能不能接着球?(如图所示)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 寿命(天) | 频数 | 频率 |
| [100,200) | 20 | 0.10 |
| [200,300) | 30 | y |
| [300,400) | 70 | 0.35 |
| [400,500) | x | 0.15 |
| [500,600) | 50 | 0.25 |
| 合计 | 200 | 1 |
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com