
【题目】如图,在三棱锥P-ABC中,![]() ,O是AC的中点,
,O是AC的中点,![]() ,
,![]() ,
,![]() .
.

(1)证明:平面![]() 平面ABC;
平面ABC;
(2)若![]() ,
,![]() ,D是AB的中点,求二面角
,D是AB的中点,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析;(2) ![]()
【解析】
(1)利用PO⊥AC,OP2+OB2=PB2,即PO⊥OB.可证明PO⊥面ABC,即可得平面PAC⊥平面ABC;
(2)由(1)得PO⊥面ABC,过O作OM⊥CD于M,连接PM,则∠PMO就是二面角P﹣CD﹣B的补角.解三角形POM即可.
(1)∵AP=CP,O是AC的中点,∴PO⊥AC,
∵PO=1,OB=2,![]() .∴OP2+OB2=PB2,即PO⊥OB.
.∴OP2+OB2=PB2,即PO⊥OB.
∵AC∩OB=O,∴PO⊥面ABC,
∵PO面PAC,∴平面PAC⊥平面ABC;
(2)由(1)得PO⊥面ABC,过O作OM⊥CD于M,连接PM,
则∠PMO就是二面角P﹣CD﹣B的平面角的补角.
∵OC![]() 1,∴AC=2,AB
1,∴AC=2,AB![]() ,∴CD
,∴CD![]() .
.
∴S△COD![]()
∴![]() ,∴OM
,∴OM![]() .PM
.PM![]() .
.
∴![]()
∴二面角P﹣CD﹣B的余弦值为![]() .
.



 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,直四棱柱ABCD–A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.

(1)证明:MN∥平面C1DE;
(2)求点C到平面C1DE的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某区的区人大代表有教师6人,分别来自甲、乙、丙、丁四个学校,其中甲校教师记为![]() ,乙校教师记为
,乙校教师记为![]() ,丙校教师记为
,丙校教师记为![]() ,丁校教师记为
,丁校教师记为![]() .现从这6名教师代表中选出3名教师组成十九大报告宣讲团,要求甲、乙、丙、丁四个学校中,每校至多选出1名.
.现从这6名教师代表中选出3名教师组成十九大报告宣讲团,要求甲、乙、丙、丁四个学校中,每校至多选出1名.
(1)请列出十九大报告宣讲团组成人员的全部可能结果;
(2)求教师![]() 被选中的概率;
被选中的概率;
(3)求宣讲团中没有乙校教师代表的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在[-4,4]上的奇函数,当x∈(0,4]时,函数的解析式为![]() (a∈R), 且
(a∈R), 且![]() .
.
(1)试求a的值;
(2)求f(x)在[-4,4]上的解析式;
(3)求f(x)在[-4,0)上的最值(最大值和最小值).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线C:![]() ,O为坐标原点,F为C的右焦点,过F的直线与C的两条渐近线的交点分别为M、N.若
,O为坐标原点,F为C的右焦点,过F的直线与C的两条渐近线的交点分别为M、N.若![]() OMN为直角三角形,则|MN|=
OMN为直角三角形,则|MN|=
A. ![]() B. 3 C.
B. 3 C. ![]() D. 4
D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 部分图象如图所示.
部分图象如图所示.
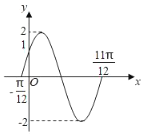
(1)求函数![]() 的解析式及
的解析式及![]() 的单调递增区间;
的单调递增区间;
(2)把函数![]() 图象上点的横坐标扩大到原来的2倍(纵坐标不变),再向左平移
图象上点的横坐标扩大到原来的2倍(纵坐标不变),再向左平移![]() 个单位,得到函数
个单位,得到函数![]() 的图象,求关于x的方程
的图象,求关于x的方程![]() 在
在![]() 上所有的实数根之和.
上所有的实数根之和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设有三个乡镇,分别位于一个矩形![]() 的两个顶点M,N及
的两个顶点M,N及![]() 的中点S处,
的中点S处,![]() ,现要在该矩形的区域内(含边界),且与M,N等距离的一点O处设一个宣讲站,记O点到三个乡镇的距离之和为
,现要在该矩形的区域内(含边界),且与M,N等距离的一点O处设一个宣讲站,记O点到三个乡镇的距离之和为![]() .
.
(1)设![]() ,试将L表示为x的函数并写出其定义域;
,试将L表示为x的函数并写出其定义域;
(2)试利用(1)的函数关系式确定宣讲站O的位置,使宣讲站O到三个乡镇的距离之和![]() 最小.
最小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量a=(cosωx-sinωx,sinωx),b=(-cosωx-sinωx,2![]() cosωx).设函数f(x)=a·b+λ(x∈R)的图象关于直线x=π对称,其中ω,λ为常数,且ω∈
cosωx).设函数f(x)=a·b+λ(x∈R)的图象关于直线x=π对称,其中ω,λ为常数,且ω∈![]() .
.
(1)求函数f(x)的最小正周期;
(2)若y=f(x)的图象经过点![]() ,求函数f(x)在区间
,求函数f(x)在区间![]() 上的取值范围
上的取值范围
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com