
分析 取BD中点O,连结EO、FO,推导出EO∥CD,且|EO|=1,FO∥AB,且|FO|=$\frac{1}{2}$,∠EOF(或其补角)是异面直线AB与CD所成的角,由此能求出EF.
解答 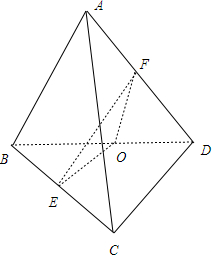 解:取BD中点O,连结EO、FO,
解:取BD中点O,连结EO、FO,
∵四面体ABCD中,|AB|=1,|CD|=2,E、F分别为BC、AD的中点,且异面直线AB与CD所成的角为60°,
∴EO∥CD,且|EO|=1,FO∥AB,且|FO|=$\frac{1}{2}$,
∴∠EOF(或其补角)是异面直线AB与CD所成的角,
∴∠EOF=60°或120°,
∴∠EOF=60°,EF=$\sqrt{\frac{1}{4}+1-2×\frac{1}{2}×1×\frac{1}{2}}$=$\frac{\sqrt{3}}{2}$,
∠EOF=120°,EF=$\sqrt{\frac{1}{4}+1+2×\frac{1}{2}×1×\frac{1}{2}}$=$\frac{\sqrt{7}}{2}$.
故答案为:$\frac{\sqrt{3}}{2}$或$\frac{{\sqrt{7}}}{2}$.
点评 本题考查线段长的求法,考查空间角,考查余弦定理的运用,不要漏掉一种情况.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ab>a2 | B. | a2<b2 | C. | $\frac{1}{a}$<$\frac{1}{b}$ | D. | $-\frac{1}{a}<-\frac{1}{b}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,AB是⊙O的直径,点C是弧$\widehat{AB}$上一点,VC垂直⊙O所在平面,D,E分别为VA,VC的中点.
如图,AB是⊙O的直径,点C是弧$\widehat{AB}$上一点,VC垂直⊙O所在平面,D,E分别为VA,VC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{1}{2}$) | B. | ($\frac{1}{2}$,+∞) | C. | (-1,$\frac{1}{2}$) | D. | ($\frac{1}{2}$,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4$\sqrt{2}$ | C. | 6 | D. | 2$\sqrt{10}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com