
| OP |
| 1 |
| 2 |
| OA |
| 1 |
| 3 |
| OB |
| AB |
| CD |
| AB |
| CD |
| AB |
| BC |
| AB |
| 1 |
| 2 |
| AB |
| AC |
| OP |
| 1 |
| 2 |
| OA |
| 1 |
| 3 |
| OB |
| 1 |
| 2 |
| 1 |
| 3 |
| AB |
| CD |
| AB |
| CD |
| ||||
|
|
| -2×3+(-1)×4 | ||
|
| -10 | ||
|
| 5 |
| AB |
| BC |
| AB |
| AB |
| BC |
| AB |
| BC |
| AB |
| 1 |
| 2 |
| AB |
| AC |


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| 1 |
| 5 |
| BC |
| CA |
| a |
| b |
| a |
| b |
| b |
| b |
| a |
| b |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 8 |
| π |
| 4 |
查看答案和解析>>
科目:高中数学 来源:学习周报 数学 人教课标版高二(A选修1-1) 2009-2010学年 第24期 总第180期 人教课标版(A选修1-1) 题型:013
下列命题中正确的是
①“若x2+y2≠0,则x,y不全为零”的否命题;
②“正多边形都相似”的逆命题;
③“若m>0,则方程x2+x-m=0有实根”的逆否命题;
④“若x=![]() 是有理数,则x是无理数”的逆否命题.
是有理数,则x是无理数”的逆否命题.
其中真命题为
①②③④
①③④
②③④
①④
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江西省赣州市十一县高二上学期期中联考理科数学试卷(带解析) 题型:填空题
给出下列命题:
(1)命题“若b2-4ac<0,则方程ax2+bx+c=0(a≠0)无实根”的否命题
(2)命题“△ABC中,AB=BC=CA,那么△ABC为等边三角形”的逆命题
(3)命题“若a>b>0,则 >
>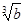 >0”的逆否命题
>0”的逆否命题
(4)“若m>1,则mx2-2(m+1)x+(m-3)>0的解集为R”的逆命题
其中真命题的序号为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com