
【选修4—4:坐标系与参数方程】
已知圆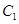 的参数方程为
的参数方程为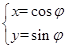 (
( 为参数),以坐标原点
为参数),以坐标原点 为极点,
为极点, 轴的正半轴为极轴建立极坐标系,圆
轴的正半轴为极轴建立极坐标系,圆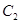 的极坐标方程为
的极坐标方程为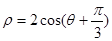 .
.
(I)将圆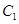 的参数方程化为普通方程,将圆
的参数方程化为普通方程,将圆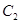 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(II)圆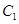 、
、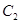 是否相交,若相交,请求出公共弦的长;若不相交,请说明理由.
是否相交,若相交,请求出公共弦的长;若不相交,请说明理由.
(I)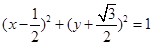 ;(II)|AB|=
;(II)|AB|=
解析试题分析:(I)由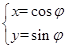 得x2+y2=1,
得x2+y2=1,
又∵ρ=2cos(θ+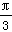 )=cosθ-
)=cosθ- sinθ,
sinθ,
∴ρ2=ρcosθ- ρsinθ.
ρsinθ.
∴x2+y2-x+ y=0,即
y=0,即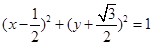
(II)圆心距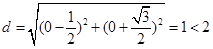 ,得两圆相交
,得两圆相交
由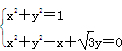 得,A(1,0),B
得,A(1,0),B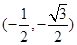 ,
,
∴|AB|=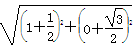 =
=
考点:本题主要考查极坐标方程与普通方程的互化,直线与圆的位置关系。
点评:中档题,学习参数方程、极坐标,其中一项基本的要求是几种不同形式方程的互化,其次是应用极坐标、参数方程,简化解题过程。参数方程的应用,往往可以把曲线问题转化成三角问题,也可在计算弦长时发挥较好作用。本题(II)利用“代数法”求弦长,也可考虑应用“特征直角三角形”,利用勾股定理求弦长。


科目:高中数学 来源: 题型:解答题
已知直线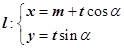 (t为参数)经过椭圆
(t为参数)经过椭圆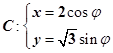 (
(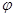 为参数)的左焦点F.
为参数)的左焦点F.
(Ⅰ)求m的值;
(Ⅱ)设直线l与椭圆C交于A、B两点,求|FA|·|FB|的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分10分)
在极坐标系中,点 坐标是
坐标是 ,曲线
,曲线 的方程为
的方程为 ;以极点为坐标原点,极轴为
;以极点为坐标原点,极轴为 轴的正半轴建立平面直角坐标系,斜率是
轴的正半轴建立平面直角坐标系,斜率是 的直线
的直线 经过点
经过点 .
.
(1)写出直线 的参数方程和曲线
的参数方程和曲线 的直角坐标方程;
的直角坐标方程;
(2)求证直线 和曲线
和曲线 相交于两点
相交于两点 、
、 ,并求
,并求 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分10分)《选修4-4:坐标系与参数方程》
在直接坐标系xOy中,直线 的方程为x-y+4=0,曲线C的参数方程为
的方程为x-y+4=0,曲线C的参数方程为
(1)已知在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,点P的极坐标为 ,判断点P与直线
,判断点P与直线 的位置关系;
的位置关系;
(2)设点Q是曲线C上的一个动点,求它到直线 的距离的最小值.
的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
某商场为了了解毛衣的月销售量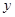 (件)与月平均气温
(件)与月平均气温 之间的关系,随机统计了某4个月的月销售量与当月平均气温,其数据如下表:
之间的关系,随机统计了某4个月的月销售量与当月平均气温,其数据如下表:
月平均气温 | 17 | 13 | 8 | 2 |
月销售量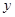 (件) (件) | 24 | 33 | 40 | 55 |
 中的
中的 =
= ,气象部门预测下个月的平均气温约为
,气象部门预测下个月的平均气温约为 ,据此估计该商场下个月毛衣销售量约为( )件.
,据此估计该商场下个月毛衣销售量约为( )件.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com