
某商场为了了解毛衣的月销售量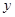 (件)与月平均气温
(件)与月平均气温 之间的关系,随机统计了某4个月的月销售量与当月平均气温,其数据如下表:
之间的关系,随机统计了某4个月的月销售量与当月平均气温,其数据如下表:
月平均气温 | 17 | 13 | 8 | 2 |
月销售量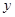 (件) (件) | 24 | 33 | 40 | 55 |
 中的
中的 =
= ,气象部门预测下个月的平均气温约为
,气象部门预测下个月的平均气温约为 ,据此估计该商场下个月毛衣销售量约为( )件.
,据此估计该商场下个月毛衣销售量约为( )件.科目:高中数学 来源: 题型:解答题
【选修4—4:坐标系与参数方程】
已知圆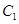 的参数方程为
的参数方程为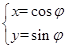 (
( 为参数),以坐标原点
为参数),以坐标原点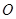 为极点,
为极点,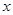 轴的正半轴为极轴建立极坐标系,圆
轴的正半轴为极轴建立极坐标系,圆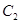 的极坐标方程为
的极坐标方程为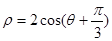 .
.
(I)将圆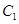 的参数方程化为普通方程,将圆
的参数方程化为普通方程,将圆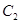 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(II)圆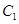 、
、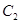 是否相交,若相交,请求出公共弦的长;若不相交,请说明理由.
是否相交,若相交,请求出公共弦的长;若不相交,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
统计某校1000名学生的数学水平测试成绩,得到样本频率分布直方图如图所示,若满分为100分,规定不低于60分为及格,则及格率是( )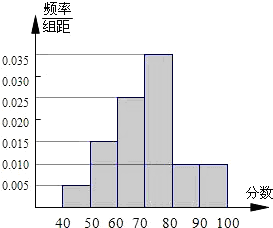
| A.20% | B.25% | C.6% | D.80% |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
在样本的频率分布直方图中,共有11个小长方形,若中间一个小长方形的面积等于其他10个小长方形面积和的 ,且样本容量为160,则中间一组的频数为( )
,且样本容量为160,则中间一组的频数为( )
| A.28 | B.32 | C.64 | D.128 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
设某大学的女生体重 (单位:
(单位: )与身高
)与身高 (单位:
(单位: )具有线性相关关系,根据一组样本数据
)具有线性相关关系,根据一组样本数据 (
(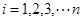 ),用最小二乘法建立的回归方程为
),用最小二乘法建立的回归方程为 ,则下列结论中不正确的是( )
,则下列结论中不正确的是( )
A. 与 与 具有正的线性相关关系 具有正的线性相关关系 |
B.回归直线过样本点的中心 |
C.若该大学某女生身高增加 ,则其体重约增加 ,则其体重约增加 |
D.若该大学某女生身高为 ,则可断定其体重为 ,则可断定其体重为 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
某全日制大学共有学生5600人,其中专科生有1300人,本科生有3000人,研究生有1300人,现采用分层抽样的方法调查学生利用因特网查找学习资料的情况,抽取的样本为280人,则应在专科生、本科生与研究生这三类学生中分别抽取( )人.
| A.65,150,65 | B.30,150,100 | C.93,94,93 | D.80,120,80 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
已知样本7,10,14,8,7,12,11,10,8,10,13,10,8,11,8,9,12,9,13,20,那么这组数据落在8.5~11.5的频率为( )
| A.0.5 | B.0.4 | C.0.3 | D.0.2 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
已知x、y的取值如下表所示:
| x | 0 | 1 | 3 | 4 |
| y | 2.2 | 4.3 | 4.8 | m |
 ,则m的值为
,则m的值为 D、6.8
D、6.8查看答案和解析>>
科目:高中数学 来源: 题型:单选题
有一个容量为66的样本,数据的分组及各组的频数如下:
[11.5,15.5) 2 [15.5,19.5) 4 [19.5,23.5) 9
[23.5,27.5) 18 [27.5,31.5) 11 [31.5,35.5) 12
[35.5,39.5) 7 [39.5,43.5) 3
根据样本的概率分布估计,大于或等于31.5的数据约占( )
A.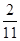 | B.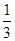 | C.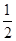 | D.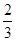 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com