
(本题满分10分)《选修4-4:坐标系与参数方程》
在直接坐标系xOy中,直线 的方程为x-y+4=0,曲线C的参数方程为
的方程为x-y+4=0,曲线C的参数方程为
(1)已知在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,点P的极坐标为 ,判断点P与直线
,判断点P与直线 的位置关系;
的位置关系;
(2)设点Q是曲线C上的一个动点,求它到直线 的距离的最小值.
的距离的最小值.
(1)点P在直线 上;(2)当
上;(2)当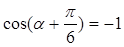 时,d取得最小值,且最小值为
时,d取得最小值,且最小值为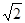 。
。
解析试题分析:(1)由曲线C的参数方程为 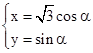 ,知曲线C的普通方程,再由点P的极坐标为(4,
,知曲线C的普通方程,再由点P的极坐标为(4, 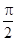 ),知点P的普通坐标为(4cos
),知点P的普通坐标为(4cos 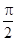 ,4sin
,4sin 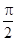 ),即(0,4),由此能判断点P与直线l的位置关系.
),即(0,4),由此能判断点P与直线l的位置关系.
(2)由Q在曲线C: 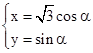 上,(0°≤α<360°),知Q(
上,(0°≤α<360°),知Q( 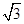 cosα,sinα)到直线l:x-y+4=0的距离d= |2sin(α+θ)+4|,(0°≤α<360°),由此能求出Q到直线l的距离的最小值
cosα,sinα)到直线l:x-y+4=0的距离d= |2sin(α+θ)+4|,(0°≤α<360°),由此能求出Q到直线l的距离的最小值
解:(1)把极坐标系下的点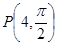 化为直角坐标,得P(0,4)。
化为直角坐标,得P(0,4)。
因为点P的直角坐标(0,4)满足直线 的方程
的方程 ,
,
所以点P在直线 上,
上,
(2)因为点Q在曲线C上,故可设点Q的坐标为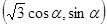 ,
,
从而点Q到直线 的距离为
的距离为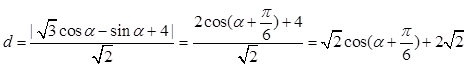
由此得,当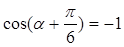 时,d取得最小值,且最小值为
时,d取得最小值,且最小值为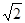
考点:本试题主要考查了椭圆的参数方程和点到直线距离公式的应用,解题时要认真审题,注意参数方程与普通方程的互化,注意三角函数的合理运用.
点评:解决该试题的关键是参数方程与普通方程的互化以及对于点到直线距离公式的灵活运用求解最值。


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:解答题
以坐标原点O为极点,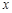 轴的正半轴为极轴建立极坐标系,曲线C1的极坐标方程为:
轴的正半轴为极轴建立极坐标系,曲线C1的极坐标方程为: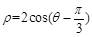 ,曲线C2的参数方程为:
,曲线C2的参数方程为: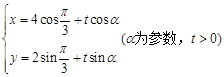 ,点N的极坐标为
,点N的极坐标为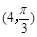 .
.
(Ⅰ)若M是曲线C1上的动点,求M到定点N的距离的最小值;
(Ⅱ)若曲线C1与曲线C2有有两个不同交点,求正数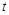 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
【选修4—4:坐标系与参数方程】
已知圆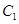 的参数方程为
的参数方程为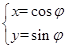 (
( 为参数),以坐标原点
为参数),以坐标原点 为极点,
为极点,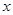 轴的正半轴为极轴建立极坐标系,圆
轴的正半轴为极轴建立极坐标系,圆 的极坐标方程为
的极坐标方程为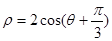 .
.
(I)将圆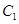 的参数方程化为普通方程,将圆
的参数方程化为普通方程,将圆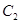 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(II)圆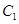 、
、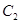 是否相交,若相交,请求出公共弦的长;若不相交,请说明理由.
是否相交,若相交,请求出公共弦的长;若不相交,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题12分) 已知曲线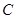
 的极坐标方程为
的极坐标方程为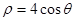 ,曲线
,曲线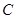
 的方程是
的方程是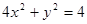 , 直线
, 直线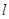 的参数方程是:
的参数方程是: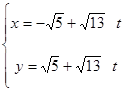
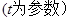 .
.
(1)求曲线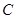
 的直角坐标方程,直线
的直角坐标方程,直线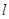 的普通方程;
的普通方程;
(2)求曲线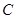
 上的点到直线
上的点到直线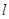 距离的最小值.
距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
选修4—4:坐标系与参数方程
在极坐标系中,曲线 ,
,
过点A(5,α)(α为锐角且 )作平行于
)作平行于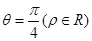 的直线
的直线 ,且
,且 与曲线L分别交于B,C两点。
与曲线L分别交于B,C两点。
(Ⅰ)以极点为原点,极轴为x轴的正半轴,取与极坐标相同单位长度,建立平面直角坐标系,写出曲线L和直线 的普通方程;
的普通方程;
(Ⅱ)求|BC|的长。
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
某小卖部销售一品牌饮料的零售价x(元/评)与销售量y(瓶)的关系统计如下:
| 零售价x(元/瓶) | 3.0 | 3.2 | 3.4 | 3.6 | 3.8 | 4.0 |
| 销量y(瓶) | 50 | 44 | 43 | 40 | 35 | 28 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
统计某校1000名学生的数学水平测试成绩,得到样本频率分布直方图如图所示,若满分为100分,规定不低于60分为及格,则及格率是( )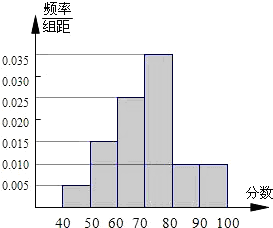
| A.20% | B.25% | C.6% | D.80% |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
在样本的频率分布直方图中,共有11个小长方形,若中间一个小长方形的面积等于其他10个小长方形面积和的 ,且样本容量为160,则中间一组的频数为( )
,且样本容量为160,则中间一组的频数为( )
| A.28 | B.32 | C.64 | D.128 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
已知x、y的取值如下表所示:
| x | 0 | 1 | 3 | 4 |
| y | 2.2 | 4.3 | 4.8 | m |
 ,则m的值为
,则m的值为 D、6.8
D、6.8查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com