
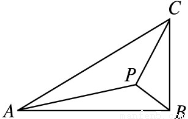
如图,在△ABC中,∠ABC=90°,AB=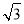 ,BC=1,P为△ABC内一点,∠BPC=90°.
,BC=1,P为△ABC内一点,∠BPC=90°.
(1)若PB= ,求PA;
,求PA;
(2)若∠APB=150°,求tan∠PBA.
(1)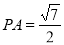 (2)
(2)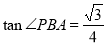
【解析】
试题分析:(1)在三角形中,两边和一角知道,该三角形是确定的,其解是唯一的,利用余弦定理求第三边.(2)利用同角三角函数的基本关系求角的正切值.(3)若是已知两边和一边的对角,该三角形具有不唯一性,通常根据大边对大角进行判断.(4)在三角兴中,注意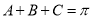 这个隐含条件的使用.
这个隐含条件的使用.
试题解析:【解析】
(1)由已知得∠PBC=60°,所以∠PBA=30°.
在△PBA中,由余弦定理得PA2=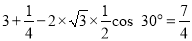 .
.
故PA=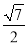 . 5分
. 5分
(2)设∠PBA=α,由已知得PB=sin α.
在△PBA中,由正弦定理得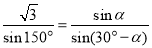 ,
,
化简得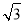 cos α=4sin α.
cos α=4sin α.
所以tan α=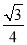 ,即tan∠PBA=
,即tan∠PBA= . 12分
. 12分
考点:(1)在三角形中正余弦定理的应用.(2)求角的三角函数.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源:2016届安徽省高一第二学期第一次月考数学试卷(解析版) 题型:选择题
已知集合M={y|y=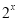 ,x>0},N={x|y=lg(2x-
,x>0},N={x|y=lg(2x-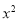 )},则M∩N为( )
)},则M∩N为( )
A.(1,2) B.(1,+∞) C.[2,+∞) D.[1,+∞)
查看答案和解析>>
科目:高中数学 来源:2016届安徽省高一下学期期末考试数学试卷(解析版) 题型:填空题
已知向量a,b满足(a+2b)·(a-b)=-6,且|a|=1,|b|=2,则a与b的夹角为 。
查看答案和解析>>
科目:高中数学 来源:2016届安徽省高一下学期期中考试数学试卷(解析版) 题型:选择题
对任意a∈[-1,1],函数f(x)=x2+(a-4)x+4-2a的值恒大于零,则x的取值范围是 ( )
A.1<x<3 B.x<1或x>3
C.1<x<2 D.x<1或x>2
查看答案和解析>>
科目:高中数学 来源:2016届安徽省高一下学期期中考试数学试卷(解析版) 题型:选择题
若不等式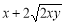
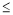 a(x+y) 对一切正数x、y恒成立,则正数a的最小值为( )
a(x+y) 对一切正数x、y恒成立,则正数a的最小值为( )
A. 1; B.  ; C. 2; D.
; C. 2; D. 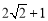 ;
;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com