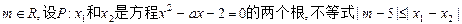练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    （12分）已知对任意实数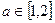恒成立；Q：函数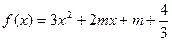有两个不同的零点. 求使“P∧Q”为真命题的实数m的取值范围.
      
    解：由题设

    当的最小值为3.
    要使对任意实数a∈[1，2]恒成立
    只须|m－5|≤3,即2≤m≤8           （6分）
    由已知，得的判别式
      （10分）
    综上，要使“P∧Q”为真命题，只需P真Q真，
    即，解得实数m的取值范围是     （12分）
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：解答题

    （本小题8分）经过调查发现，某种新产品在投放市场的30天中,前20天其价格直线上升，后10天价格呈直线下降趋势。现抽取其中4天的价格如下表所示：
    时间
    		第4天
    		第12天
    		第20天
    		第28天
    价格
    (千元)
    		34
    		42
    		50
    		34
     
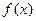    （1）写出价格关于时间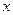的函数表达式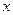（表示投放市场的第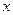天）
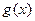    （2）若销售量与时间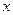的函数关系式为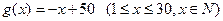：，问该产品投放市场第几天，日销售额最高?

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （本小题满分15分）
    若函数f(x)＝ax3＋bx2＋cx＋d是奇函数，且f(x)极小值＝f(－)＝－．
    （1）求函数f(x)的解析式；
    （2）求函数f(x)在[－1，m](m＞－1)上的最大值；
    （3）设函数g(x)＝，若不等式g(x)·g(2k－x)≥(－k)2在(0，2k)上恒成立，求实数k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

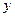    （本小题满分12分）张家界某景区为提高经济效益，现对某一景点进行改造升级，从而扩大内需，提高旅游增加值，经过市场调查，旅游增加值万元与投入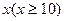万元之间满足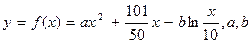：为常数。当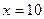万元时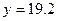，万元；当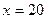万元时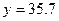，万元。（参考数据：）
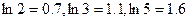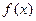    （1）求的解析式；
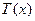    （2）求该景点改造升级后旅游利润的最大值。（利润=旅游增加值-投入）

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    周期为4的函数其中m>0，若方程3f(x)=x恰有5个实数解，则m的取值范围为     （  ）
    A．B．C．D．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    函数的图象是以原点为圆心，1为半径的两段圆弧，则不等式的解集为      （   ）
    A．B．C．D．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

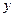    某学校要招开学生代表大会，规定各班每10人推选一名代表，当各班人数除以10的余数大于6时再增选一名代表.那么，各班可推选代表人数与该班人数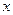之间的函数关系用取整函数y＝[x]（[x]表示不大于x的最大整数）可以表示为（ ）
    A．y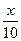＝[]B．y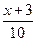＝[]C．y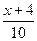＝[]D．y＝[]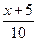

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    已知函数，正实数是公差为正数的等差数列，且满足．若实数是方程的一个解，那么下列四个判断：①；②；③；④中有可能成立的个数为      

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    若一系列函数的解析式相同，值域相同，但是定义域不同，则称这些函数为“同族函数”。那么解析式为，值域是｛1，4｝的“同族函数”有    个。

    查看答案和解析>>

    同步练习册答案