练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    15．执行如图所示的程序框图，则输出的S的值为（　　）
    A．-2015B．2016C．2014D．-2017

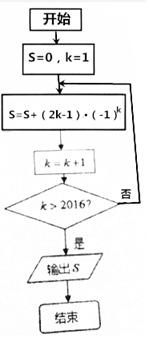
    分析 分析程序中各变量、各语句的作用，再根据流程图所示的顺序，可知：该程序的作用是累加并输出S=-1+3-…+-2015+2016的值．

    解答 解：分析程序中各变量、各语句的作用，
    再根据流程图所示的顺序，可知：
    该程序的作用是累加并输出S=-1+3-…+-2015+2016=2016．
    故选B

    点评 根据流程图（或伪代码）写程序的运行结果，是算法这一模块最重要的题型，其处理方法是：：①分析流程图（或伪代码），从流程图（或伪代码）中既要分析出计算的类型，又要分析出参与计算的数据（如果参与运算的数据比较多，也可使用表格对数据进行分析管理）⇒②建立数学模型，根据第一步分析的结果，选择恰当的数学模型③解模．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

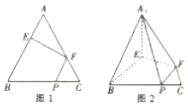    15．在边长为3的正三角形ABC中，E，F，P分别是AB，AC，BC边上的点，满足$\frac{AE}{EB}$=$\frac{CF}{FA}$=$\frac{CP}{PB}$=$\frac{1}{2}$，将△AEF沿EF折起到△A1EF的位置，使二面角A1-EF-B成直二面角，连结A1B，A1P（如图），则以下结论错误的是（　　）
    A．CF∥平面A1EP
    B．A1E⊥平面BEP
    C．点B到面A1PF的距离为$\sqrt{3}$
    D．异面直线BP与A1F所成角的余弦值为$\frac{3}{4}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．设g（x）=ex，f（x）=g[λx+（1-λ）a]-λg（x），其中a，λ是常数，且0＜λ＜1．
    （1）求函数f（x）的极值；
    （2）证明：对任意正数a，存在正数x，使不等式|$\frac{{e}^{x}-1}{x}-1$|＜a成立．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．在锐角△ABC中，∠A=$\frac{π}{3}$，∠BAC的平分线交边BC于点D，|AD|=1，则△ABC面积的取值范围是（　　）
    A．[$\frac{\sqrt{10}}{6}$，$\frac{\sqrt{7}}{4}$]B．[$\frac{\sqrt{3}}{3}$，$\frac{\sqrt{7}}{4}$]C．[$\frac{\sqrt{10}}{6}$，$\frac{3\sqrt{3}}{8}$）D．[$\frac{\sqrt{3}}{3}$，$\frac{3\sqrt{3}}{8}$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．在平面直角坐标系xOy中，直线l过点P（-1，2），倾斜角为$\frac{3π}{4}$．以坐标原点为极点，x轴正半轴为极轴，取相同的单位长度建立极坐标系，曲线C的极坐标方程为ρ=4cosθ．
    （1）写出直线l的参数方程和曲线C的直角坐标方程；
    （2）记直线l和曲线C的两个交点分别为A，B，求|PA|+|PB|，|PA|•|PB|

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．已知双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右支上存在一点M，使得|PQ|=|MQ|，其中P（-b，0），Q（b，0），若tan∠MQP=-2$\sqrt{2}$，则双曲线C的渐近线方程为y=±$\frac{\sqrt{41}}{5}$x．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．若2x=9，${log_2}\frac{8}{3}=y$，则x+2y=6．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．复数$z=\frac{3-i}{1-i}$的共轭复数是2-i．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．已知f（x）=2|x|+x2，若f（a-1）≤3，则a的取值范围是[0，2]．

    查看答案和解析>>

    同步练习册答案