
| A. | [$\frac{\sqrt{10}}{6}$,$\frac{\sqrt{7}}{4}$] | B. | [$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{7}}{4}$] | C. | [$\frac{\sqrt{10}}{6}$,$\frac{3\sqrt{3}}{8}$) | D. | [$\frac{\sqrt{3}}{3}$,$\frac{3\sqrt{3}}{8}$) |
分析 根据余弦定理和角平分线定理,求出△ABC是正三角形时面积取得最小值$\frac{\sqrt{3}}{3}$,当AB⊥BC时,△ABC面积取得最大值$\frac{3\sqrt{3}}{8}$,由此求出结果.
解答 解:如图所示,
锐角△ABC中,∠A=$\frac{π}{3}$,∠BAC的平分线交边BC于点D,|AD|=1,
根据余弦定理,BD2=c2+1-2c•cos$\frac{π}{6}$=c2-$\sqrt{3}$c+1,
CD2=b2+1-2b•cos$\frac{π}{6}$=b2-$\sqrt{3}$b+1;
根据角平分线定理,$\frac{DB}{CD}$=$\frac{AB}{AC}$,
即$\frac{{c}^{2}-\sqrt{3}c+1}{{b}^{2}-\sqrt{3}b+1}$=$\frac{{c}^{2}}{{b}^{2}}$;
∴b2c2-$\sqrt{3}$b2c+b2=b2c2-$\sqrt{3}$bc2+c2,
即$\sqrt{3}$bc(c-b)=(c-b)(c+b);
当b=c时,△ABC是正三角形,由|AD|=1,
得AB=AC=$\frac{2}{\sqrt{3}}$,则S△ABC=$\frac{1}{2}$bcsin$\frac{π}{3}$=$\frac{\sqrt{3}}{3}$;
当b≠c时,$\sqrt{3}$bc=b+c≥2$\sqrt{bc}$,当且仅当b=c时“=”成立,
所以bc≥$\frac{4}{3}$,即b=c=$\frac{2}{\sqrt{3}}$时S△ABC取得最小值为$\frac{\sqrt{3}}{3}$;
又当AB⊥BC时,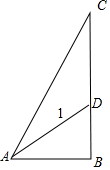
BD=$\frac{1}{2}$,AB=$\frac{\sqrt{3}}{2}$,DC=AD=1,
S△ABC=$\frac{1}{2}$×$\frac{\sqrt{3}}{2}$×(1+$\frac{1}{2}$)=$\frac{3\sqrt{3}}{8}$为最大值,
△ABC面积的取值范围是[$\frac{\sqrt{3}}{3}$,$\frac{3\sqrt{3}}{8}$].
故选:D.
点评 本题考查了解三角形的应用问题,也考查了三角形面积的计算问题,是较难的题目.


科目:高中数学 来源: 题型:选择题
| A. | 60° | B. | 120° | C. | 135° | D. | 150° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图所示为棱长为1的正方体的表面展开图,在原正方体中,给出下列四个结论:
如图所示为棱长为1的正方体的表面展开图,在原正方体中,给出下列四个结论:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 患慢性气管炎 | 未患慢性气管炎 | 合计 | |
| 吸烟 | 20 | 20 | 40 |
| 不吸烟 | 5 | 55 | 60 |
| 合计 | 25 | 75 | 100 |
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{512}$ | B. | -$\frac{341}{512}$ | C. | $\frac{1}{1024}$ | D. | $\frac{1}{2048}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com