
【题目】已知f(x)是R上的奇函数且单调递增,则下列函数是偶函数且在(0,+∞)上单调递增的有( )
①y=|f(x)|;
②y=f(x2+x);
③y=f(|x|);
④y=ef(x)+e﹣f(x).
A.①②③B.①③④C.②③④D.①②④
【答案】B
【解析】
由已知可得f(x)是R上的奇函数且单调递增,当x>0时,f(x)>f(0)=0,然后结合函数的性质分别进行检验即可.
因为f(x)是R上的奇函数且单调递增,
故当x>0时,f(x)>f(0)=0,
①g(﹣x)=|f(﹣x)|=|f(x)|=g(x)为偶函数,且当x>0时,g(x)=|f(x)|=f(x)单调递增,符合题意;
②g(﹣x)=f(x2﹣x)≠g(x),故不满足偶函数;
③g(﹣x)=f(|﹣x|)=f(|x|)=g(x)为偶函数,且 x>0时g(x)=f(x)单调递增,符合题意;
④g(﹣x)=ef(﹣x)+e﹣f(﹣x)=e﹣f(x)+ef(x)=g(x),满足偶函数,且x>0时,f(x)>0,ef(x)>1,因为![]() 在
在![]() 单调递增,
单调递增,
由复合函数的单调性可知g(x)=ef(x)+e﹣f(x)单调递增,符合题意.
故选:B.
本题主要考查函数的奇偶性和单调性的应用,还考查了转化求解问题的能力,属于中档题.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 上任意一点到其两个焦点
上任意一点到其两个焦点![]() ,
,![]() 的距离之和等于
的距离之和等于![]() ,且圆
,且圆![]() 经过椭圆的焦点.
经过椭圆的焦点.
(1)求椭圆的方程;
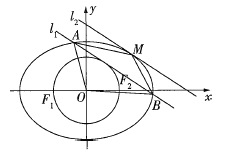
(2)如图,若直线![]() 与圆O相切,且与椭圆相交于A,B两点,直线
与圆O相切,且与椭圆相交于A,B两点,直线![]() 与
与![]() 平行且与椭圆相切于点M(O,M位于直线
平行且与椭圆相切于点M(O,M位于直线![]() 的两侧).记
的两侧).记![]() ,
,![]() 的面积分别为
的面积分别为![]() ,
,![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市208年抽样100户居民的月均用电量(单位:千瓦时),以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分组,得到如下频率分布表:
分组,得到如下频率分布表:
分组 | 频数 | 频率 |
|
| 0.04 |
| 19 |
|
|
| 0.22 |
| 25 | 0.25 |
| 15 | 0.15 |
| 10 |
|
| 5 | 0.05 |
(1)求表中![]() 的值,并估计2018年该市居民月均用电量的中位数
的值,并估计2018年该市居民月均用电量的中位数![]() ;
;
(2)该城市最近十年的居民月均用电量逐年上升,以当年居民月均用电量的中位数![]() (单位:千瓦时)作为统计数据,下图是部分数据的折线图.
(单位:千瓦时)作为统计数据,下图是部分数据的折线图.
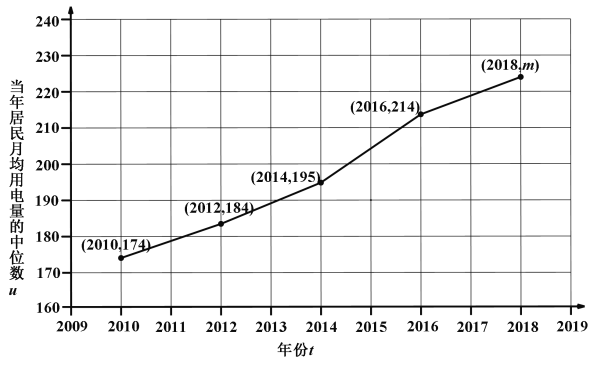
由折线图看出,可用线性回归模型拟合![]() 与年份
与年份![]() 的关系.
的关系.
①为简化运算,对以上数据进行预处理,令![]() ,
,![]() ,请你在答题卡上完成数据预处理表;
,请你在答题卡上完成数据预处理表;
②建立![]() 关于
关于![]() 的线性回归方程,预测2020年该市居民月均用电量的中位数.
的线性回归方程,预测2020年该市居民月均用电量的中位数.
附:回归直线![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为: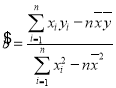 ,
,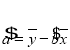 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在全面建成小康社会的决胜阶段,让贫困地区同全国人民共同进入全面小康社会是我们党的庄严承诺.在“脱真贫、真脱贫”的过程中,精准扶贫助推社会公平显得尤其重要.若某农村地区有200户贫困户,经过一年扶贫后,对该地区的“精准扶贫”的成效检查验收.从这200户贫困户中随机抽出50户,对各户的人均年收入(单位:千元)进行调查得到如下频数表:
人均年收入 |
|
|
|
|
|
|
频数 | 2 | 3 | 10 | 20 | 10 | 5 |
若人均年收入在4000元以下的判定为贫困户,人均年收入在4000元~8000元的判定为脱贫户,人均年收入达到8000元的判定为小康户.
(1)用样本估计总体,估计该地区还有多少户没有脱贫;
(2)为了了解未脱贫的原因,从抽取的50户中用分层抽样的方法抽10户进行调研.
①贫困户、脱贫户、小康户分别抽到的人数是多少?
②从被抽到的脱贫户和小康户中各选1人做经验介绍,求小康户中人均年收入最高的一户被选到的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直三棱柱ABC﹣A1B1C1中,AB⊥BC,BB1![]() BC,D是CC1的中点.
BC,D是CC1的中点.

(1)证明:B1C⊥平面ABD;
(2)若AB=BC,E是A1C1的中点,求二面角A﹣BD﹣E的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年第十三届女排世界杯共12支参赛球队,比赛赛制釆取单循环方式,即每支球队进行11场比赛,最后靠积分选出最后冠军.积分规则如下(比赛采取5局3胜制):比赛中以3—0或3—1取胜的球队积3分,负队积0分;而在比赛中以3—2取胜的球队积2分,负队积1分.9轮过后,积分榜上的前2名分别为中国队和美国队,中国队积26分,美国队积22分.第10轮中国队对抗塞尔维亚队,设每局比赛中国队取胜的概率为![]() .
.
(1)第10轮比赛中,记中国队3—1取胜的概率为![]() ,求
,求![]() 的最大值点
的最大值点![]() .
.
(2)以(1)中的![]() 作为
作为![]() 的值.
的值.
(i)在第10轮比赛中,中国队所得积分为![]() ,求
,求![]() 的分布列;
的分布列;
(ⅱ)已知第10轮美国队积3分,判断中国队能否提前一轮夺得冠军(第10轮过后,无论最后一轮即第11轮结果如何,中国队积分最多)?若能,求出相应的概率;若不能,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】体温是人体健康状况的直接反应,一般认为成年人腋下温度T(单位:![]() )平均在
)平均在![]() 之间即为正常体温,超过
之间即为正常体温,超过![]() 即为发热.发热状态下,不同体温可分成以下三种发热类型:低热:
即为发热.发热状态下,不同体温可分成以下三种发热类型:低热:![]() ;高热:
;高热:![]() ;超高热(有生命危险):
;超高热(有生命危险):![]() .某位患者因患肺炎发热,于12日至26日住院治疗.医生根据病情变化,从14日开始,以3天为一个疗程,分别用三种不同的抗生素为该患者进行消炎退热.住院期间,患者每天上午8:00服药,护士每天下午16:00为患者测量腋下体温记录如下:
.某位患者因患肺炎发热,于12日至26日住院治疗.医生根据病情变化,从14日开始,以3天为一个疗程,分别用三种不同的抗生素为该患者进行消炎退热.住院期间,患者每天上午8:00服药,护士每天下午16:00为患者测量腋下体温记录如下:
抗生素使用情况 | 没有使用 | 使用“抗生素A”疗 | 使用“抗生素B”治疗 | |||||
日期 | 12日 | 13日 | 14日 | 15日 | 16日 | 17日 | 18日 | 19日 |
体温( | 38.7 | 39.4 | 39.7 | 40.1 | 39.9 | 39.2 | 38.9 | 39.0 |
抗生素使用情况 | 使用“抗生素C”治疗 | 没有使用 | |||||
日期 | 20日 | 21日 | 22日 | 23日 | 24日 | 25日 | 26日 |
体温( | 38.4 | 38.0 | 37.6 | 37.1 | 36.8 | 36.6 | 36.3 |
(I)请你计算住院期间该患者体温不低于![]() 的各天体温平均值;
的各天体温平均值;
(II)在19日—23日期间,医生会随机选取3天在测量体温的同时为该患者进行某一特殊项目“a项目”的检查,记X为高热体温下做“a项目”检查的天数,试求X的分布列与数学期望;
(III)抗生素治疗一般在服药后2-8个小时就能出现血液浓度的高峰,开始杀灭细菌,达到消炎退热效果.假设三种抗生素治疗效果相互独立,请依据表中数据,判断哪种抗生素治疗效果最佳,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com