
【题目】已知椭圆![]() 上任意一点到其两个焦点
上任意一点到其两个焦点![]() ,
,![]() 的距离之和等于
的距离之和等于![]() ,且圆
,且圆![]() 经过椭圆的焦点.
经过椭圆的焦点.
(1)求椭圆的方程;
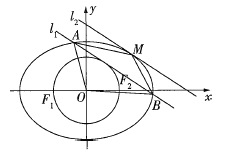
(2)如图,若直线![]() 与圆O相切,且与椭圆相交于A,B两点,直线
与圆O相切,且与椭圆相交于A,B两点,直线![]() 与
与![]() 平行且与椭圆相切于点M(O,M位于直线
平行且与椭圆相切于点M(O,M位于直线![]() 的两侧).记
的两侧).记![]() ,
,![]() 的面积分别为
的面积分别为![]() ,
,![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)已知椭圆![]() 上任意一点到其两个焦点
上任意一点到其两个焦点![]() ,
,![]() 的距离之和等于
的距离之和等于![]() ,可得
,可得![]() ,圆
,圆![]() 经过椭圆的焦点,求得
经过椭圆的焦点,求得![]() ,即可求得椭圆的方程;
,即可求得椭圆的方程;
(2)由于![]() 与圆
与圆![]() 相切,可得
相切,可得![]() ,联立椭圆和
,联立椭圆和![]() 方程,由直线
方程,由直线![]() 与椭圆相切,可得
与椭圆相切,可得![]() ,根据三角形面积公式求得
,根据三角形面积公式求得![]() ,
,![]() ,进而求得
,进而求得![]() 的取值范围.
的取值范围.
(1)![]() 已知椭圆
已知椭圆![]() 上任意一点到其两个焦点
上任意一点到其两个焦点![]() ,
,![]() 的距离之和等于
的距离之和等于![]()
由椭圆定义可得![]() ,
,
![]()
![]() .
.
![]()
![]()
![]() 椭圆
椭圆![]() 的焦点在
的焦点在![]() 上
上
![]() 圆
圆![]() 与
与![]() 交点为
交点为![]()
又![]() 圆
圆![]() 经过椭圆的焦点
经过椭圆的焦点
![]() 可得椭圆
可得椭圆![]()
![]()
![]() ,
,
故椭圆方程为![]() .
.
(2)由于![]() 与圆
与圆![]() 相切,
相切,
根据点到直线距离公式可得圆![]() 的圆心到直线的距离为:
的圆心到直线的距离为:![]() ,
,
即![]() .
.
设直线![]() 的方程为
的方程为![]() ,
,
联立椭圆和![]() 方程,可得
方程,可得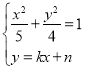 消去y,
消去y,
可得:![]() ,
,
![]() 直线
直线![]() 与椭圆相切,
与椭圆相切,
![]()
![]() ,整理得
,整理得![]() .
.
直线![]() 与
与![]() 之间的距离
之间的距离![]() ,
,![]() ,
,![]() ,
,
![]()
![]() .
.
可得: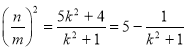 .
.
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
又![]()
![]() ,
,![]() 位于直线
位于直线![]() 的两侧,
的两侧,
![]() m,n同号,
m,n同号,
![]()
![]() ,
,
![]()
![]() ,
,![]() ,
,
故![]() 的取值范围是:
的取值范围是:![]() .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且以椭圆上的点和长轴两端点为顶点的三角形的面积的最大值为
,且以椭圆上的点和长轴两端点为顶点的三角形的面积的最大值为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)经过定点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于不同的两点
于不同的两点![]() 、
、![]() ,点
,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,试证明:直线
,试证明:直线![]() 与
与![]() 轴的交点
轴的交点![]() 为一个定点,且
为一个定点,且![]() (
(![]() 为原点).
为原点).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD﹣A1B1C1D1中,M,N,P分别是C1D1,BC,A1D1的中点,有下列四个结论:
①AP与CM是异面直线;②AP,CM,DD1相交于一点;③MN∥BD1;
④MN∥平面BB1D1D.
其中所有正确结论的编号是( )

A.①④B.②④C.①④D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某晚会上某歌舞节目的表演者是3个女孩和4个男孩.演出结束后,7个人合影留念(3个人站在前排,4个人站在后排),其中男孩甲、乙要求站在一起,女孩丙不能站在两边,不同站法的种数为( )
A.96B.240C.288D.432
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 分别是椭圆
分别是椭圆![]()
![]()
![]() 的左右焦点,其焦距为
的左右焦点,其焦距为![]() ,过
,过![]() 的直线与
的直线与![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() 的周长是
的周长是![]() .
.
(1)求![]() 的方程;
的方程;
(2)若![]() 是
是![]() 上的动点,从点
上的动点,从点![]() (
(![]() 是坐标系原点)向圆
是坐标系原点)向圆![]() 作两条切线,分别交
作两条切线,分别交![]() 于
于![]() ,
,![]() 两点.已知直线
两点.已知直线![]() ,
,![]() 的斜率存在,并分别记为
的斜率存在,并分别记为![]() ,
,![]() .
.
(ⅰ)求证:![]() 为定值;
为定值;
(ⅱ)试问![]() 是否为定值?若是,求出该值;若不是,请说明理由.
是否为定值?若是,求出该值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年新年伊始,新型冠状病毒来势汹汹,疫情使得各地学生在寒假结束之后无法返校,教育部就此提出了线上教学和远程教学,停课不停学的要求也得到了家长们的赞同.各地学校开展各式各样的线上教学,某地学校为了加强学生爱国教育,拟开设国学课,为了了解学生喜欢国学是否与性别有关,该学校对100名学生进行了问卷调查,得到如下列联表:
喜欢国学 | 不喜欢国学 | 合计 | |
男生 | 20 | 50 | |
女生 | 10 | ||
合计 | 100 |
(1)请将上述列联表补充完整,并判断能否在犯错误的概率不超过0.001的前提下认为喜欢国学与性别有关系?
(2)针对问卷调查的100名学生,学校决定从喜欢国学的人中按分层抽样的方法随机抽取6人成立国学宣传组,并在这6人中任选2人作为宣传组的组长,设这两人中女生人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
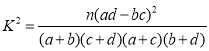 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是R上的奇函数且单调递增,则下列函数是偶函数且在(0,+∞)上单调递增的有( )
①y=|f(x)|;
②y=f(x2+x);
③y=f(|x|);
④y=ef(x)+e﹣f(x).
A.①②③B.①③④C.②③④D.①②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com