
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且以椭圆上的点和长轴两端点为顶点的三角形的面积的最大值为
,且以椭圆上的点和长轴两端点为顶点的三角形的面积的最大值为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)经过定点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于不同的两点
于不同的两点![]() 、
、![]() ,点
,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,试证明:直线
,试证明:直线![]() 与
与![]() 轴的交点
轴的交点![]() 为一个定点,且
为一个定点,且![]() (
(![]() 为原点).
为原点).
科目:高中数学 来源: 题型:
【题目】口袋中有大小、形状、质地相同的两个白球和三个黑球.现有一抽奖游戏规则如下:抽奖者每次有放回的从口袋中随机取出一个球,最多取球2n+1(n![]() )次.若取出白球的累计次数达到n+1时,则终止取球且获奖,其它情况均不获奖.记获奖概率为
)次.若取出白球的累计次数达到n+1时,则终止取球且获奖,其它情况均不获奖.记获奖概率为![]() .
.
(1)求![]() ;
;
(2)证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】交强险是车主必须为机动车购买的险种,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系.每年交强险最终保险费计算方法是:交强险最终保险费![]() ,其中a为交强险基础保险费,A为与道路交通事故相联系的浮动比率,同时满足多个浮动因素的,按照向上浮动或者向下浮动比率的高者计算.按照我国《机动车交通事故责任强制保险基础费率表》的规定:普通6座以下私家车的交强险基础保险费
,其中a为交强险基础保险费,A为与道路交通事故相联系的浮动比率,同时满足多个浮动因素的,按照向上浮动或者向下浮动比率的高者计算.按照我国《机动车交通事故责任强制保险基础费率表》的规定:普通6座以下私家车的交强险基础保险费![]() 为950元,交强险费率浮动因素及比率如下表:
为950元,交强险费率浮动因素及比率如下表:
交强险浮动因素和浮动费率比率表 | ||
类型 | 浮动因素 | 浮动比率 |
| 上一个年度未发生有责任道路交通事故 |
|
| 上两个年度未发生有责任道路交通事故 |
|
| 上三个及以上年度未发生有责任道路交通事故 |
|
| 上一个年度发生一次有责任不涉及死亡的道路交通事故 |
|
| 上一个年度发生两次及以上有责任道路交通事故 |
|
| 上一个年度发生有责任道路交通死亡事故 |
|
某机构为了研究某一品牌普通6座以下私家车的投保情况,随机抽取了100辆车龄已满三年的该品牌同型号私家车的下一年续保时的情况,统计结果如下表:
类型 |
|
|
|
|
|
|
数量 | 25 | 10 | 10 | 25 | 20 | 10 |
以这100辆该品牌车的投保类型的频率代替一辆车投保类型的概率,完成下列问题.
(1)记X为一辆该品牌车在第四年续保时的费用,求X的分布列与数学期望(数学期望值保留到个位数字);
(2)某二手车销售商专门销售这一品牌的二手车,且将经销商购车后下一年的交强险最终保险费高于交强险基础保险费![]() 的车辆记为事故车,假设购进一辆事故车亏损3000元,购进一辆非事故车盈利5000元.
的车辆记为事故车,假设购进一辆事故车亏损3000元,购进一辆非事故车盈利5000元.
①若该销售商购进三辆(车龄已满三年)该品牌二手车,求这三辆车中至少有一辆是事故车的概率;
②若该销售商一次购进100辆(车龄已满三年)该品牌二手车,求他获得利润的期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且四个顶点构成的四边形的面积是
,且四个顶点构成的四边形的面积是![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知直线![]() 经过点
经过点![]() ,且不垂直于
,且不垂直于![]() 轴,直线
轴,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 为
为![]() 的中点,直线
的中点,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点(
两点(![]() 是坐标原点),若四边形
是坐标原点),若四边形![]() 的面积为
的面积为![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 则x∈[﹣1,e]时,f(x)的最小值为_____;设g(x)=[f(x)]2﹣f(x)+a若函数g(x)有6个零点,则实数a的取值范围是_____.
则x∈[﹣1,e]时,f(x)的最小值为_____;设g(x)=[f(x)]2﹣f(x)+a若函数g(x)有6个零点,则实数a的取值范围是_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】区块链技术被认为是继蒸汽机、电力、互联网之后,下一代颠覆性的核心技术区块链作为构造信任的机器,将可能彻底改变整个人类社会价值传递的方式,2015年至2019年五年期间,中国的区块链企业数量逐年增长,居世界前列现收集我国近5年区块链企业总数量相关数据,如表
年份 | 2015 | 2016 | 2017 | 2018 | 2019 |
编号 | 1 | 2 | 3 | 4 | 5 |
企业总数量y(单位:千个) | 2.156 | 3.727 | 8.305 | 24.279 | 36.224 |
注:参考数据![]() (其中z=lny).
(其中z=lny).
附:样本(xi,yi)(i=1,2,…,n)的最小二乘法估计公式为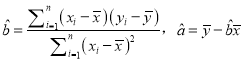
(1)根据表中数据判断,y=a+bx与y=cedx(其中e=2.71828…,为自然对数的底数),哪一个回归方程类型适宜预测未来几年我国区块链企业总数量?(给出结果即可,不必说明理由)
(2)根据(1)的结果,求y关于x的回归方程(结果精确到小数点后第三位);
(3)为了促进公司间的合作与发展,区块链联合总部决定进行一次信息化技术比赛,邀请甲、乙、丙三家区块链公司参赛比赛规则如下:①每场比赛有两个公司参加,并决出胜负;②每场比赛获胜的公司与未参加此场比赛的公司进行下一场的比赛;③在比赛中,若有一个公司首先获胜两场,则本次比赛结束,该公司就获得此次信息化比赛的“优胜公司”,已知在每场比赛中,甲胜乙的概率为![]() ,甲胜丙的概率为
,甲胜丙的概率为![]() ,乙胜丙的概率为
,乙胜丙的概率为![]() ,请通过计算说明,哪两个公司进行首场比赛时,甲公司获得“优胜公司”的概率最大?
,请通过计算说明,哪两个公司进行首场比赛时,甲公司获得“优胜公司”的概率最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 上任意一点到其两个焦点
上任意一点到其两个焦点![]() ,
,![]() 的距离之和等于
的距离之和等于![]() ,且圆
,且圆![]() 经过椭圆的焦点.
经过椭圆的焦点.
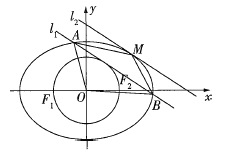
(1)求椭圆的方程;
(2)如图,若直线![]() 与圆O相切,且与椭圆相交于A,B两点,直线
与圆O相切,且与椭圆相交于A,B两点,直线![]() 与
与![]() 平行且与椭圆相切于点M(O,M位于直线
平行且与椭圆相切于点M(O,M位于直线![]() 的两侧).记
的两侧).记![]() ,
,![]() 的面积分别为
的面积分别为![]() ,
,![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com