
分析 (1)根据所给条件,待定系数法求解b与c;
(2)据上一问的结果,将原不等式整理为m<g(x)恒成立,当x∈[-1,1],所以转化为求函数g(x)在给定区间的最小值问题.
解答 解:(1)由f(0)=f(-2),
则c=4-2b+c,即b=2.再有f(1)=3=1+b+c,则c=0,
故f(x)=x2+2x;
(2)由f(x)>x+m恒成立,则x2+2x>x+m;
∴x2+x>m,
令g(x)=x2+x,故g(x)在区间[-1,1]上的最小值为g(-$\frac{1}{2}$)=-$\frac{1}{4}$,
∴m<-$\frac{1}{4}$.
点评 1.待定系数求函数的解析式;2.二次函数求最值和恒成立问题的转化.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{3}$-y2=1 | B. | x2-$\frac{{y}^{2}}{3}$=1 | C. | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{2}$=1 | D. | $\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{3}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
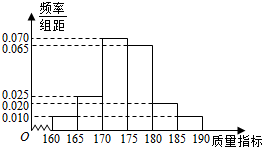 从某企业的一种产品中抽取40件产品,测量其某项质量指标,测量结果的频率分布直方图如图所示.
从某企业的一种产品中抽取40件产品,测量其某项质量指标,测量结果的频率分布直方图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 600 | B. | 450 | C. | 300 | D. | 150 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分类 人数(人) 时间 | 一小时以上 | 一小时以内 | 不使用 | 合计 |
| 上课时间 | 23 | 55 | m | 98 |
| 不上课时间 | 17 | 68 | 17 | 102 |
| 合计 | 40 | 123 | n | 200 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com