Question

【题目】如图，点在以为直径的上运动，平面，且，点分别是、的中点．

（1）求证：；

（2）若，求点平面的距离．

Answer 1

【答案】（1）见解析；（2）

【解析】

（1）证明平面可得，再结合即可得出平面，故而；（2）取中点，过作于，则可证平面，从而即为所求．

（1）证明：∵PA⊥平面ABC，BC平面ABC，

∴PA⊥BC，

∵AB是圆的直径，∴BC⊥AC，

又AC∩PA=A，

∴BC⊥平面PAC，

又PC平面PAC．

∴BC⊥PC，

∵DE是△PBC的中位线，∴DE∥BC，

∴PC⊥DE，

∵PA=AC，D是PC的中点，

∴AD⊥PC，

又AD∩DE=D，

∴PC⊥平面ADE，又AE平面ADE，

∴PC⊥AE．

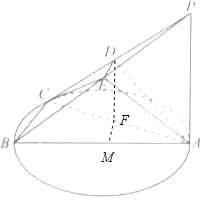
（2）解：取AC中点F，过F作FM⊥AB于M，

∵D，F分别是PC，AC的中点，

∴DF∥PA，又DF平面PAB，PA平面PAB，

∴DF∥平面PAB，

∴D到平面PAB的距离等于F到平面PAB的距离．

∵PA⊥平面ABC，FM平面ABC，

∴FM⊥PA，又FM⊥AB，PA∩AB=A，

∴FM⊥平面PAB，

∴F到平面PAB的距离为线段FM的长．

在Rt△ABC中，∵AB=2AC=2，∴AC=，

∴C到AB的距离为=，

又F为AC的中点，∴FM=．

∴点D到平面PAB的距离为．