
【题目】如图,在矩形纸片![]() 中,
中,![]() ,
,![]() ,在线段
,在线段![]() 上取一点
上取一点![]() ,沿着过
,沿着过![]() 点的直线将矩形右下角折起,使得右下角顶点
点的直线将矩形右下角折起,使得右下角顶点![]() 恰好落在矩形的左边
恰好落在矩形的左边![]() 边上.设折痕所在直线与
边上.设折痕所在直线与![]() 交于
交于![]() 点,记折痕
点,记折痕![]() 的长度为
的长度为![]() ,翻折角
,翻折角![]() 为
为![]() .
.

(1)探求![]() 与
与![]() 的函数关系,推导出用
的函数关系,推导出用![]() 表示
表示![]() 的函数表达式;
的函数表达式;
(2)设![]() 的长为
的长为![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)确定点![]() 在何处时,翻折后重叠部分的图形面积最小.
在何处时,翻折后重叠部分的图形面积最小.
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦距为2,过点
的焦距为2,过点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设椭圆的右焦点为F,定点![]() ,过点F且斜率不为零的直线l与椭圆交于A,B两点,以线段AP为直径的圆与直线
,过点F且斜率不为零的直线l与椭圆交于A,B两点,以线段AP为直径的圆与直线![]() 的另一个交点为Q,证明:直线BQ恒过一定点,并求出该定点的坐标.
的另一个交点为Q,证明:直线BQ恒过一定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(k+![]() )lnx+
)lnx+![]() ,k∈[4,+∞),曲线y=f(x)上总存在两点M(x1,y1),N(x2,y2),使曲线y=f(x)在M,N两点处的切线互相平行,则x1+x2的取值范围为
,k∈[4,+∞),曲线y=f(x)上总存在两点M(x1,y1),N(x2,y2),使曲线y=f(x)在M,N两点处的切线互相平行,则x1+x2的取值范围为
A. (![]() ,+∞) B. (
,+∞) B. (![]() ,+∞) C. [
,+∞) C. [![]() ,+∞) D. [
,+∞) D. [![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(k+![]() )lnx+
)lnx+![]() ,k∈[4,+∞),曲线y=f(x)上总存在两点M(x1,y1),N(x2,y2),使曲线y=f(x)在M,N两点处的切线互相平行,则x1+x2的取值范围为
,k∈[4,+∞),曲线y=f(x)上总存在两点M(x1,y1),N(x2,y2),使曲线y=f(x)在M,N两点处的切线互相平行,则x1+x2的取值范围为
A. (![]() ,+∞) B. (
,+∞) B. (![]() ,+∞) C. [
,+∞) C. [![]() ,+∞) D. [
,+∞) D. [![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省高考改革实施方案指出:该省高考考生总成绩将由语文、数学、外语3门统一高考成绩和学生自主选择的学业水平等级性考试科目共同构成.该省教育厅为了解正就读高中的学生家长对高考改革方案所持的赞成态度,随机从中抽取了100名城乡家长作为样本进行调查,调查结果显示样本中有25人持不赞成意见.下面是根据样本的调查结果绘制的等高条形图.
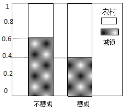
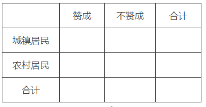
(1)根据已知条件与等高条形图完成下面的2×2列联表,并判断我们能否有95%的把握认为“赞成高考改革方案与城乡户口有关”?
(2)利用分层抽样从持“不赞成”意见家长中抽取5名参加学校交流活动,从中选派2名家长发言,求恰好有1名城镇居民的概率.
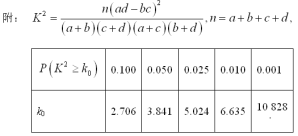
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙、丁四人进行一项益智游戏,方法如下:第一步:先由四人看着平面直角坐标系中方格内的16个棋子(如图所示),甲从中记下某个棋子的坐标;第二步:甲分别告诉其他三人:告诉乙棋子的横坐标.告诉丙棋子的纵坐标,告诉丁棋子的横坐标与纵坐标相等;第三步:由乙、丙、丁依次回答.对话如下:“乙先说我无法确定.丙接着说我也无法确定.最后丁说我知道”.则甲记下的棋子的坐标为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com