
【题目】已知椭圆![]() 的焦距为2,过点
的焦距为2,过点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设椭圆的右焦点为F,定点![]() ,过点F且斜率不为零的直线l与椭圆交于A,B两点,以线段AP为直径的圆与直线
,过点F且斜率不为零的直线l与椭圆交于A,B两点,以线段AP为直径的圆与直线![]() 的另一个交点为Q,证明:直线BQ恒过一定点,并求出该定点的坐标.
的另一个交点为Q,证明:直线BQ恒过一定点,并求出该定点的坐标.
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:
【题目】环保部门要对所有的新车模型进行广泛测试,以确定它的行车里程的等级,右表是对 100 辆新车模型在一个耗油单位内行车里程(单位:公里)的测试结果.
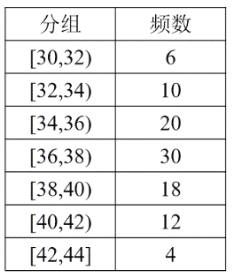
(Ⅰ)做出上述测试结果的频率分布直方图,并指出其中位数落在哪一组;
(Ⅱ)用分层抽样的方法从行车里程在区间[38,40)与[40,42)的新车模型中任取5辆,并从这5辆中随机抽取2辆,求其中恰有一个新车模型行车里程在[40,42)内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在矩形纸片![]() 中,
中,![]() ,
,![]() ,在线段
,在线段![]() 上取一点
上取一点![]() ,沿着过
,沿着过![]() 点的直线将矩形右下角折起,使得右下角顶点
点的直线将矩形右下角折起,使得右下角顶点![]() 恰好落在矩形的左边
恰好落在矩形的左边![]() 边上.设折痕所在直线与
边上.设折痕所在直线与![]() 交于
交于![]() 点,记折痕
点,记折痕![]() 的长度为
的长度为![]() ,翻折角
,翻折角![]() 为
为![]() .
.

(1)探求![]() 与
与![]() 的函数关系,推导出用
的函数关系,推导出用![]() 表示
表示![]() 的函数表达式;
的函数表达式;
(2)设![]() 的长为
的长为![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)确定点![]() 在何处时,翻折后重叠部分的图形面积最小.
在何处时,翻折后重叠部分的图形面积最小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com