
【题目】已知函数f(x)=(k+![]() )lnx+
)lnx+![]() ,k∈[4,+∞),曲线y=f(x)上总存在两点M(x1,y1),N(x2,y2),使曲线y=f(x)在M,N两点处的切线互相平行,则x1+x2的取值范围为
,k∈[4,+∞),曲线y=f(x)上总存在两点M(x1,y1),N(x2,y2),使曲线y=f(x)在M,N两点处的切线互相平行,则x1+x2的取值范围为
A. (![]() ,+∞) B. (
,+∞) B. (![]() ,+∞) C. [
,+∞) C. [![]() ,+∞) D. [
,+∞) D. [![]() ,+∞)
,+∞)
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源: 题型:
【题目】我国在北宋1084年第一次印刷出版了《算经十书》,即贾宪的《黄帝九章算法细草》,刘益的《议古根源》,秦九韶的《数书九章》,李冶的《测圆海镜》和《益古演段》,杨辉的《详解九章算法》、《日用算法》和《杨辉算法》,朱世杰的《算学启蒙》和《四元玉鉴》.这些书中涉及的很多方面都达到古代数学的高峰,其中一些“算法”如开立方和开四次方也是当时世界数学的高峰.某图书馆中正好有这十本书现在小明同学从这十本书中任借两本阅读,那么他取到的书的书名中有“算”字的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着城市地铁建设的持续推进,市民的出行也越来越便利.根据大数据统计,某条地铁线路运行时,发车时间间隔t(单位:分钟)满足:4≤t≤15,![]() N,平均每趟地铁的载客人数p(t)(单位:人)与发车时间间隔t近似地满足下列函数关系:
N,平均每趟地铁的载客人数p(t)(单位:人)与发车时间间隔t近似地满足下列函数关系: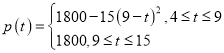 ,其中
,其中![]() .
.
(1)若平均每趟地铁的载客人数不超过1500人,试求发车时间间隔t的值.
(2)若平均每趟地铁每分钟的净收益为![]() (单位:元),问当发车时间间隔t为多少时,平均每趟地铁每分钟的净收益最大?井求出最大净收益.
(单位:元),问当发车时间间隔t为多少时,平均每趟地铁每分钟的净收益最大?井求出最大净收益.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,某游乐园的一个摩天轮半径为10米,轮子的底部在地面上2米处,如果此摩天轮每20分钟转一圈,当摩天轮上某人经过![]() 处时开始计时(按逆时针方向转),
处时开始计时(按逆时针方向转),![]() (其中
(其中![]() 平行于地面).
平行于地面).
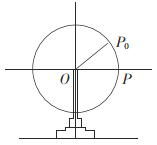
(1)求开始转动5分钟时此人相对于地面的高度.
(2)开始转动![]() 分钟时,摩天轮上此人经过点
分钟时,摩天轮上此人经过点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在△ABC中,D,E分别为AB,AC的中点,O为DE的中点,AB=AC=2![]() ,BC=4.将△ADE沿DE折起到△A1DE的位置,使得平面A1DE
,BC=4.将△ADE沿DE折起到△A1DE的位置,使得平面A1DE![]() 平面BCED,如下图.
平面BCED,如下图.

(Ⅰ)求证:A1O![]() BD;
BD;
(Ⅱ)求直线A1C和平面A1BD所成角的正弦值;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com