
【题目】已知命题p: ![]() <1,q:x2+(a﹣1)x﹣a>0,若p是q的充分不必要条件,则实数a的取值范围是( )
<1,q:x2+(a﹣1)x﹣a>0,若p是q的充分不必要条件,则实数a的取值范围是( )
A.(﹣2,﹣1]
B.[﹣2,﹣1]
C.[﹣3,﹣1]
D.[﹣2,+∞)
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知一个递增的等差数列{an}的前三项的和为﹣3,前三项的积为8.数列 ![]() 的前n项和为
的前n项和为 ![]() .
.
(1)求数列{an}的通项公式.
(2)求数列 ![]() 的通项公式.
的通项公式.
(3)是否存在一个等差数列{cn},使得等式 ![]() 对所有的正整数n都成立.若存在,求出所有满足条件的等差数列{cn}的通项公式,并求数列{bn}的前n项和Tn;若不存在,请说明理由.
对所有的正整数n都成立.若存在,求出所有满足条件的等差数列{cn}的通项公式,并求数列{bn}的前n项和Tn;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数y=Asin(ωx+φ)在一个周期内的图象如图,此函数的解析式为( ) 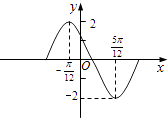
A.y=2sin(2x+ ![]() )
)
B.y=2sin(2x+ ![]() )
)
C.y=2sin( ![]() ﹣
﹣ ![]() )
)
D.y=2sin(2x﹣ ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设关于某设备的使用年限x(年)和所支出的维修费用y(万元)有如下的统计资料:
x | 2 | 3 | 4 | 5 | 6 |
y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
(1)画出散点图并判断是否线性相关;
(2)如果线性相关,求线性回归方程;
(3)估计使用年限为10年时,维修费用是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设Ox、Oy是平面内相交成45°角的两条数轴, ![]() 、
、 ![]() 分别是x轴、y轴正方向同向的单位向量,若向量
分别是x轴、y轴正方向同向的单位向量,若向量 ![]() =x
=x ![]() +y
+y ![]() ,则把有序数对(x,y)叫做向量
,则把有序数对(x,y)叫做向量 ![]() 在坐标系xOy中的坐标,在此坐标系下,假设
在坐标系xOy中的坐标,在此坐标系下,假设 ![]() =(﹣2,2
=(﹣2,2 ![]() ),
), ![]() =(2,0),
=(2,0), ![]() =(5,﹣3
=(5,﹣3 ![]() ),则下列命题不正确的是( )
),则下列命题不正确的是( ) 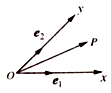
A.![]() =(1,0)
=(1,0)
B.| ![]() |=2
|=2 ![]()
C.![]() ∥
∥ ![]()
D.![]() ⊥
⊥ ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:数列{an}前n项的乘积Tn=a1a2…an , 数列an=29﹣n , 则下面的等式中正确的是( )
A.T1=T19
B.T3=T17
C.T5=T12
D.T8=T11
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD为矩形,且AD=2,AB=1,PA⊥平面ABCD,E为BC上的动点. 
(1)当E为BC的中点时,求证:PE⊥DE;
(2)设PA=1,在线段BC上存在这样的点E,使得二面角P﹣ED﹣A的平面角大小为 ![]() .试确定点E的位置.
.试确定点E的位置.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com