练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】函数y=Asin（ωx+φ）在一个周期内的图象如图，此函数的解析式为（ ）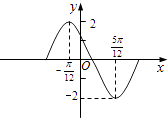
    A.y=2sin（2x+ ）
    B.y=2sin（2x+ ）
    C.y=2sin（ ﹣ ）
    D.y=2sin（2x﹣ ）

    【答案】A
    【解析】解：由已知可得函数y=Asin（ωx+）的图象经过（﹣ ，2）点和（﹣ ，2）

    则A=2，T=π即ω=2

    则函数的解析式可化为y=2sin（2x+），将（﹣ ，2）代入得

    ﹣ += +2kπ，k∈Z，

    即φ= +2kπ，k∈Z，

    当k=0时，φ=

    此时

    故选A

    根据已知中函数y=Asin（ωx+）在一个周期内的图象经过（﹣ ，2）和（﹣ ，2），我们易分析出函数的最大值、最小值、周期，然后可以求出A，ω，φ值后，即可得到函数y=Asin（ωx+）的解析式．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】下列有关命题的说法中错误的是（ ）
    A.若p或q为假命题，则p、q均为假命题．
    B.“x=1”是“x2﹣3x+2=0”的充分不必要条件．
    C.命题“若x2﹣3x+2=0，则x=1”的逆否命题为：“若x≠1，则x2﹣3x+2≠0”．
    D.对于命题p：存在x∈R使得x2+x+1＜0，则非p：存在x∈R，使x2+x+1≥0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知△ABC的三个内角A，B，C的对边分别是a，b，c，且bcosC=（2a﹣c）cosB．
    （1）求角B．
    （2）若 ，△ABC的周长为 ，求△ABC的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知f（x）= x3﹣2x2+3x﹣m
    （1）求f（x）的极值
    （2）当m取何值时，函数f（x）有三个不同零点？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示的多面体，它的正视图为直角三角形，侧视图为正三角形，俯视图为正方形（尺寸如图所示），E为VB的中点．
    （1）求证：VD∥平面EAC；
    （2）求二面角A﹣VB﹣D的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知命题p： ＜1，q：x2+（a﹣1）x﹣a＞0，若p是q的充分不必要条件，则实数a的取值范围是（ ）
    A.（﹣2，﹣1]
    B.[﹣2，﹣1]
    C.[﹣3，﹣1]
    D.[﹣2，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，锐角α和钝角β的终边分别与单位圆交于A，B两点．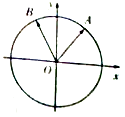
    （I）若A，B两点的纵会标分别为 的值；
    （II）已知点C是单位圆上的一点，且 的夹角θ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在如图所示的多面体中，EF⊥平面AEB，AE⊥EB，AD∥EF，EF∥BC．BC=2AD=4，EF=3，AE=BE=2，G为BC的中点．
    （1）求证：AB∥平面DEG；
    （2）求证：BD⊥EG；
    （3）求二面角C﹣DF﹣E的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】四面体ABCD及其三视图如图1，2所示．

    （1）求四面体ABCD的体积；
    （2）若点E为棱BC的中点，求异面直线DE和AB所成角的余弦值．

    查看答案和解析>>

    同步练习册答案