
分析 (1)由题意可得 A-B∈(0,$\frac{π}{2}$),利用正弦定理求得tanB 的值,可得sinB和cosB的值,求得cosA=cos[(A-B)+B]的值,可得sinA的值,
从而求得sinBsinA的值.
(2)求得cosC=-cos(A+B)=-(cosAcosB-sinAsinB)的值,可得cosC+cosA 的值.
解答 解:(1)△ABC中,由于a=5,b=4,a>b,∴A-B∈(0,$\frac{π}{2}$),
∵sin(A-B)=$\frac{3\sqrt{7}}{32}$,∴cos(A-B)=$\frac{31}{32}$.
由正弦定理可得$\frac{5}{sinA}$=$\frac{4}{sinB}$,
求得sinA=$\frac{5}{4}$sinB=sin[(A-B)+B]=sin(A-B)cosB+cos(A-B)sinB=$\frac{3\sqrt{7}}{32}$cosB+$\frac{31}{32}$sinB.
∴$\frac{9}{32}$sinB=$\frac{31}{32}$cosB,即3sinB=$\sqrt{7}$cosB,tanB=$\frac{\sqrt{7}}{3}$,∴sinB=$\frac{\sqrt{7}}{4}$,∴cosB=$\frac{3}{4}$.
cosA=cos[(A-B)+B]=cos(A-B)cosB+sin(A-B)sinB=$\frac{31}{32}•\frac{3}{4}$+$\frac{3\sqrt{7}}{32}•\frac{\sqrt{7}}{4}$=$\frac{9}{16}$,∴sinA=$\frac{5\sqrt{7}}{16}$,
故sinBsinA=$\frac{\sqrt{7}}{4}•\frac{5\sqrt{7}}{16}$=$\frac{35}{64}$.
(2)cosC=-cos(A+B)=-(cosAcosB-sinAsinB)=-($\frac{9}{16}•\frac{3}{4}$-$\frac{5\sqrt{7}}{16}•\frac{\sqrt{7}}{4}$)=$\frac{1}{8}$,
∴cosC+cosA=$\frac{1}{8}$+$\frac{9}{16}$=$\frac{11}{16}$.
点评 本题主要考查两角和差的三角公式,同角三角函数的基本关系,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
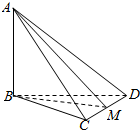
| A. | ∠ADB | B. | ∠BDC | C. | ∠AMB | D. | ∠ACB |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
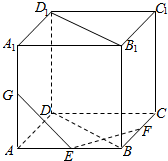 如图,在棱长为2的正方体ABCD一A1B1C1D1中,点E,F,G分别是边AB,BC,AA1上的点,记AE=x,BF=y,A1G=z,
如图,在棱长为2的正方体ABCD一A1B1C1D1中,点E,F,G分别是边AB,BC,AA1上的点,记AE=x,BF=y,A1G=z,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,已知正方体ABCD-A1B1C1D1的棱长为2,P是底面ABCD内一动点,且满足PC⊥PD,则当P运动时,A1P2的最小值是( )
如图,已知正方体ABCD-A1B1C1D1的棱长为2,P是底面ABCD内一动点,且满足PC⊥PD,则当P运动时,A1P2的最小值是( )| A. | 12-2$\sqrt{2}$ | B. | 12+2$\sqrt{2}$ | C. | 10+2$\sqrt{5}$ | D. | 10-2$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 0 | C. | -3 | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 不喜欢数学课程 | 喜欢数学课程 | 总计 | |
| 男 | 45 | 10 | 55 |
| 女 | 30 | 15 | 45 |
| 总 | 75 | 25 | 100 |
| P(K2≥k0) | 0.10 | 0.05 | 0.025 |
| k0 | 2.706 | 3.841 | 5.024 |
| A. | 有90%以上的把握认为“性别与是否喜欢数学课程有关” | |
| B. | 有90%以上的把握认为“性别与是否喜欢数学课程没有关” | |
| C. | 在犯错误的概率不超过1%的前提下,认为“性别与是否喜欢数学课程有关” | |
| D. | 在犯错误的概率不超过1%的前提下,认为“性别与是否喜欢数学课程没有关” |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com