
【题目】已知f(x)是定义域为(0,+∞)的单调函数,若对任意的x∈(0,+∞),都有 ![]() ,且方程|f(x)﹣3|=x3﹣6x2+9x﹣4+a在区间(0,3]上有两解,则实数a的取值范围是( )
,且方程|f(x)﹣3|=x3﹣6x2+9x﹣4+a在区间(0,3]上有两解,则实数a的取值范围是( )
A.0<a≤5
B.a<5
C.0<a<5
D.a≥5
【答案】A
【解析】解:∵定义域为(0,+∞)的单调函数f(x)
满足f[f(x)+log ![]() x]=4,
x]=4,
∴必存在唯一的正实数a,
满足f(x)+log ![]() x=a,f(a)=4,①
x=a,f(a)=4,①
∴f(a)+log ![]() a=a,②
a=a,②
由①②得:4+log ![]() a=a,log
a=a,log ![]() a=a﹣4,
a=a﹣4,
a=( ![]() )a﹣4,左增,右减,有唯一解a=3,
)a﹣4,左增,右减,有唯一解a=3,
故f(x)+log ![]() x=a=3,
x=a=3,
f(x)=3﹣log ![]() x,
x,
由方程|f(x)﹣3|=x3﹣6x2+9x﹣4+a在区间(0,3]上有两解,
即有|log ![]() x|=x3﹣6x2+9x﹣4+a,
x|=x3﹣6x2+9x﹣4+a,
由g(x)=x3﹣6x2+9x﹣4+a,g′(x)=3x2﹣12x+9=3(x﹣1)(x﹣3),
当1<x<3时,g′(x)<0,g(x)递减;当0<x<1时,g′(x)<0,g(x)递增.
g(x)在x=1处取得最大值a,g(0)=a﹣4,g(3)=a﹣4,
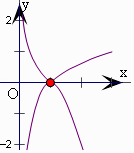
分别作出y=|log ![]() x|,和y=x3﹣6x2+9x﹣4的图象,可得
x|,和y=x3﹣6x2+9x﹣4的图象,可得
两图象只有一个交点,将y=x3﹣6x2+9x﹣4的图象向上平移,
至经过点(3,1),有两个交点,
由g(3)=1即a﹣4=1,解得a=5,
当0<a≤5时,两图象有两个交点,
即方程|f(x)﹣3|=x3﹣6x2+9x﹣4+a在区间(0,3]上有两解.
故选:A.
由题设知必存在唯一的正实数a,满足f(x)+log ![]() x=a,f(a)=4,f(a)+log
x=a,f(a)=4,f(a)+log ![]() a=a,故4+log
a=a,故4+log ![]() a=a,log
a=a,log ![]() a=a﹣4,a=(
a=a﹣4,a=( ![]() )a﹣4,左增,右减,有唯一解a=3,故f(x)+log
)a﹣4,左增,右减,有唯一解a=3,故f(x)+log ![]() x=a=3,由题意可得|log
x=a=3,由题意可得|log ![]() x|=x3﹣6x2+9x﹣4+a在区间(0,3]上有两解,讨论g(x)=x3﹣6x2+9x﹣4+a的单调性和最值,分别画出作出y=|log
x|=x3﹣6x2+9x﹣4+a在区间(0,3]上有两解,讨论g(x)=x3﹣6x2+9x﹣4+a的单调性和最值,分别画出作出y=|log ![]() x|,和y=x3﹣6x2+9x﹣4的图象,通过平移即可得到a的范围.
x|,和y=x3﹣6x2+9x﹣4的图象,通过平移即可得到a的范围.


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系 ![]() 中,点
中,点 ![]() 在抛物线
在抛物线 ![]() 上.
上.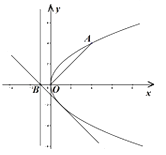
(1)求 ![]() 的方程和
的方程和 ![]() 的焦点的坐标;
的焦点的坐标;
(2)设点 ![]() 为准线与
为准线与 ![]() 轴的交点,直线
轴的交点,直线 ![]() 过点
过点 ![]() ,且与直线
,且与直线 ![]() 垂直,求证:
垂直,求证: ![]() 与
与 ![]() 相切.
相切.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={3,a2},集合B={0,b,1﹣a},且A∩B={1},则A∪B=( )
A.{0,1,3}
B.{1,2,4}
C.{0,1,2,3}
D.{0,1,2,3,4}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx,g(x)= ![]() ﹣
﹣ ![]() (x为实常数).
(x为实常数).
(1)当a=1时,求函数φ(x)=f(x)﹣g(x)在x∈[4,+∞)上的最小值;
(2)若方程e2f(x)=g(x)(其中e=2.71828…)在区间[ ![]() ]上有解,求实数a的取值范围.
]上有解,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|x<2},B={x|3﹣2x>0},则( )
A.A∩B={x|x< ![]() }
}
B.A∩B=?
C.A∪B={x|x< ![]() }
}
D.AUB=R
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】几位大学生响应国家的创业号召,开发了一款应用软件.为激发大家学习数学的兴趣,他们推出了“解数学题获取软件激活码”的活动.这款软件的激活码为下面数学问题的答案:已知数列1,1,2,1,2,4,1,2,4,8,1,2,4,8,16,…,其中第一项是20 , 接下来的两项是20 , 21 , 再接下来的三项是20 , 21 , 22 , 依此类推.求满足如下条件的最小整数N:N>100且该数列的前N项和为2的整数幂.那么该款软件的激活码是( )
A.440
B.330
C.220
D.110
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com