
【题目】如图,在三棱柱![]() 中,
中,![]() 是棱
是棱![]() 的中点.
的中点.

(1)证明:![]() 平面
平面![]() ;
;
(2)若![]() 是棱
是棱![]() 的中点,求三棱锥
的中点,求三棱锥![]() 的体积与三棱柱
的体积与三棱柱![]() 的体积之比.
的体积之比.
【答案】(1)见解析;(2)![]()
【解析】
(1)连接AC1交A1C于点O,连接OD,由中位线定理可得OD∥BC1,故而BC1∥平面A1CD;(2)根据棱锥和棱柱的体积公式即可得出结论.
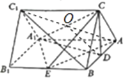
(1)证明:连接AC1交A1C于点O,连接OD,
∵CC1∥AA1,CC1=AA1,
∴四边形AA1C1C是平行四边形,
∴O是AC1的中点,又D是AB的中点,
∴OD∥BC1,又OD平面A1CD,BC1平面A1CD,
∴BC1∥平面A1CD.
(2)设三棱柱A1B1C1﹣ABC的高为h,则三棱柱A1B1C1﹣ABC的体积V=S△ABCh,
又V=V![]() V
V![]() ,V
,V![]() V
V![]() S△ABCh
S△ABCh![]() ,
,
∴V![]() ,
,
∵CC1∥BB1,CC1平面ABB1A1,BB1平面ABB1A1,
∴CC1∥平面ABB1A1,
∴V![]() V
V![]() ,
,
∵S![]() S
S![]() ,∴V
,∴V![]() V
V![]() ,
,
∴三棱锥C﹣AA1E的体积与三棱柱A1B1C1﹣ABC的体积之比为![]() .
.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,设
,设![]() 的外接圆圆心为
的外接圆圆心为![]() .
.

(1)若![]() 与直线
与直线![]() 相切,求实数
相切,求实数![]() 的值;
的值;
(2)设点![]() 在
在![]() 上,使
上,使![]() 的面积等于12的点
的面积等于12的点![]() 有且只有三个,试问这样的
有且只有三个,试问这样的![]() 是否存在?若存在求出
是否存在?若存在求出![]() 的标准方程;若不存在,说明理由.
的标准方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体的底面与正四面体的底面在同一平面α上,且AB∥CD,正方体的六个面所在的平面与直线CE,EF相交的平面个数分别记为m,n,那么m+n=( ) 
A.8
B.9
C.10
D.11
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小波以游戏方式决定是参加学校合唱团还是参加学校排球队,游戏规则为:以0为起点,再从A1 , A2 , A3 , A4 , A5 , A6 , A7 , A8(如图)这8个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为X.若X=0就参加学校合唱团,否则就参加学校排球队. 
(1)求小波参加学校合唱团的概率;
(2)求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,直线![]() 的参数方程为
的参数方程为 (其中
(其中![]() 为参数).现以坐标原点为极点,
为参数).现以坐标原点为极点, ![]() 轴的非负半轴为极轴建立极坐标标系,曲线
轴的非负半轴为极轴建立极坐标标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;(2)求直线
的直角坐标方程;(2)求直线![]() 被曲线
被曲线![]() 截得的线段的长度.
截得的线段的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角坐标系![]() 中,圆
中,圆![]() 与
与![]() 轴负半轴交于点
轴负半轴交于点![]() ,过点
,过点![]() 的直线
的直线![]() ,
,![]() 分别与圆
分别与圆![]() 交于
交于![]() ,
,![]() 两点.
两点.

(Ⅰ)若![]() ,
,![]() ,求
,求![]() 的面积;
的面积;
(Ⅱ)若直线![]() 过点
过点![]() ,证明:
,证明:![]() 为定值,并求此定值.
为定值,并求此定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3+ax2+bx+c,下列结论中错误的是( )
A.xα∈R,f(xα)=0
B.函数y=f(x)的图象是中心对称图形
C.若xα是f(x)的极小值点,则f(x)在区间(﹣∞,xα)单调递减
D.若xα是f(x)的极值点,则f′(xα)=0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直棱柱ABC﹣A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB= ![]() AB.
AB. 
(1)证明:BC1∥平面A1CD
(2)求二面角D﹣A1C﹣E的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com