
已知![]() ,点
,点![]() 满足
满足![]() ,记点
,记点![]() 的轨迹为
的轨迹为![]() .
.
(Ⅰ)求轨迹![]() 的方程;(Ⅱ)若直线
的方程;(Ⅱ)若直线![]() 过点
过点![]() 且与轨迹
且与轨迹![]() 交于
交于![]() 、
、![]() 两点. (i)设点
两点. (i)设点![]() ,问:是否存在实数
,问:是否存在实数![]() ,使得直线
,使得直线![]() 绕点
绕点![]() 无论怎样转动,都有
无论怎样转动,都有![]() 成立?若存在,求出实数
成立?若存在,求出实数![]() 的值;若不存在,请说明理由.(ii)过
的值;若不存在,请说明理由.(ii)过![]() 、
、![]() 作直线
作直线![]() 的垂线
的垂线![]() 、
、![]() ,垂足分别为
,垂足分别为![]() 、
、![]() ,记
,记
![]() ,求
,求![]() 的取值范围.
的取值范围.
(Ⅰ)![]()
(Ⅰ)由![]()
![]() 知,点
知,点![]() 的轨迹
的轨迹![]() 是以
是以![]() 、
、![]() 为焦点的双曲线右支,由
为焦点的双曲线右支,由![]() ,∴
,∴![]() ,故轨迹E的方程为
,故轨迹E的方程为![]() …………3分
…………3分
(Ⅱ)当直线l的斜率存在时,设直线l方程为![]() ,与双曲线方程联立消
,与双曲线方程联立消![]() 得
得![]() ,设
,设![]() 、
、![]() ,
,
∴ , 解得
, 解得![]() ……………5分
……………5分
|

![]() ……………………7分
……………………7分
假设存在实数![]() ,使得
,使得![]() ,
,
故得![]() 对任意的
对任意的![]() 恒成立,
恒成立,
∴ ,解得
,解得![]() ∴当
∴当![]() 时,
时,![]() .
.
当直线l的斜率不存在时,由![]() 及
及![]() 知结论也成立,
知结论也成立,
综上,存在![]() ,使得
,使得![]() . …………………………………………8分
. …………………………………………8分
(ii)∵![]() ,∴直线
,∴直线![]() 是双曲线的右准线,…………………………9分
是双曲线的右准线,…………………………9分
由双曲线定义得:![]() ,
,![]() ,
,
方法一:∴

![]() …………………………………………10分
…………………………………………10分
∵![]() ,∴
,∴![]() ,∴
,∴![]() ………………………………………11分
………………………………………11分
注意到直线的斜率不存在时,![]() ,综上,
,综上, …………………12分
…………………12分
|
与双曲线右支有二个交点,∴![]() ,过
,过![]()
作![]() ,垂足为
,垂足为![]() ,则
,则![]() ,
,
∴![]()
 …(10分)
…(10分)
由![]() ,得
,得![]() 故:
故: …(12分)
…(12分)


科目:高中数学 来源:2011-2012学年广西省高三第二次模拟考试理科数学试卷 题型:解答题
已知 ,
, ,点
,点 满足
满足 ,记点
,记点 的轨迹为
的轨迹为 ,过点
,过点 作直线
作直线 与轨迹
与轨迹 交于
交于 两点,过
两点,过 作直线
作直线 的垂线
的垂线 、
、 ,垂足分别为
,垂足分别为 ,记
,记 。
。
(1)求轨迹 的方程;
的方程;
(2)设点 ,求证:当
,求证:当 取最小值时,
取最小值时, 的面积为
的面积为 .
.
查看答案和解析>>
科目:高中数学 来源:2011年辽宁省锦州市高二第一学期末理科数学卷 题型:解答题
(本小题满分12分)
已知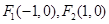 ,点
,点 满足
满足 ,记点
,记点 的轨迹为
的轨迹为 .
.
(Ⅰ)求轨迹 的方程;
的方程;
(Ⅱ)过点F2(1,0)作直线l与轨迹 交于不同的两点A、B,设
交于不同的两点A、B,设 ,若
,若 的取值范围
的取值范围
查看答案和解析>>
科目:高中数学 来源:2010-2011学年上海市奉贤区高三第一学期调研测试数学文理合卷 题型:解答题
(文)已知 ,点
,点 满足
满足 ,记点
,记点 的轨迹为E,
的轨迹为E,
(1)、求轨迹E的方程;(5分)
(2)、如果过点Q(0,m)且方向向量为 =(1,1) 的直线l与点P的轨迹交于A,B两点,当
=(1,1) 的直线l与点P的轨迹交于A,B两点,当 时,求
时,求 AOB的面积。(9分)
AOB的面积。(9分)
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分)
已知![]() ,点
,点![]() 满足
满足![]() ,记点
,记点![]() 的轨迹为
的轨迹为![]() .
.
(Ⅰ)求轨迹![]() 的方程;
的方程;
(Ⅱ)过点F2(1,0)作直线l与轨迹![]() 交于不同的两点A、B,设
交于不同的两点A、B,设![]() ,若
,若![]() 的取值范围。
的取值范围。
|

|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com